Exam - Lone Star College
... Answer: C 17) f(x) = x 3 + 8x2 - x - 8 A) 8, multiplicity 1, crosses the x-axis; 1, multiplicity 1, crosses the x-axis; - 8, multiplicity 1, crosses the x-axis. B) -1, multiplicity 1, touches the x-axis and turns around; 1, multiplicity 1, touches the x-axis and turns around; - 8, multiplicity 1, to ...
... Answer: C 17) f(x) = x 3 + 8x2 - x - 8 A) 8, multiplicity 1, crosses the x-axis; 1, multiplicity 1, crosses the x-axis; - 8, multiplicity 1, crosses the x-axis. B) -1, multiplicity 1, touches the x-axis and turns around; 1, multiplicity 1, touches the x-axis and turns around; - 8, multiplicity 1, to ...
Lectures on Integer Partitions - Penn Math
... Integer partitions were first studied by Euler. For many years one of the most intriguing and difficult questions about them was determining the asymptotic properties of p(n) as n got large. This question was finally answered quite completely by Hardy, Ramanujan, and Rademacher [11, 16] and their re ...
... Integer partitions were first studied by Euler. For many years one of the most intriguing and difficult questions about them was determining the asymptotic properties of p(n) as n got large. This question was finally answered quite completely by Hardy, Ramanujan, and Rademacher [11, 16] and their re ...
older, more formal version
... where there are m copies of Z/n. So the answer to our question is yes. However, this last step is not entirely satisfying, since we have just repeated the same group over and over again. We could instead ask if there are more interesting ways to obtain such a groupoid. For example, could we instead ...
... where there are m copies of Z/n. So the answer to our question is yes. However, this last step is not entirely satisfying, since we have just repeated the same group over and over again. We could instead ask if there are more interesting ways to obtain such a groupoid. For example, could we instead ...
Sets, Infinity, and Mappings - University of Southern California
... The term elements emphasizes that the objects of a set can be viewed as its smallest “atomic” pieces. The union of all pieces forms the whole set. The set A defined in (4) is a 3-element set (it consists of 3 objects). The set B defined in (5) is a 2-element set. The term members is useful when sets ...
... The term elements emphasizes that the objects of a set can be viewed as its smallest “atomic” pieces. The union of all pieces forms the whole set. The set A defined in (4) is a 3-element set (it consists of 3 objects). The set B defined in (5) is a 2-element set. The term members is useful when sets ...
Introduction to Database Systems
... for each y Y, f-1(y) has at most k elements, then X has at most k * n(Y) elements There are 42 students who are to share 12 computers. Each student uses exactly 1 computer and no computer is used by more than 6 students. Show that at least 5 computers are used by 3 or more students. Melikyan/DM/Fal ...
... for each y Y, f-1(y) has at most k elements, then X has at most k * n(Y) elements There are 42 students who are to share 12 computers. Each student uses exactly 1 computer and no computer is used by more than 6 students. Show that at least 5 computers are used by 3 or more students. Melikyan/DM/Fal ...
Chapter 9 Section 1
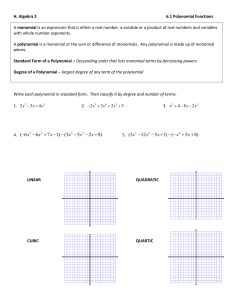
... Polynomial: The sum of one or more monomials is called a polynomial. Monomial: A monomial is a number, a variable, or a product of numbers and variables that have only positive exponents. Binomial: A polynomial with two terms is a binomial. Trinomial: A polynomial with three terms is a trinomial. ...
... Polynomial: The sum of one or more monomials is called a polynomial. Monomial: A monomial is a number, a variable, or a product of numbers and variables that have only positive exponents. Binomial: A polynomial with two terms is a binomial. Trinomial: A polynomial with three terms is a trinomial. ...
Full text
... Tp(n) = "£sp(k) is the number of binomial coefficients in the first n rows of Pascal's triangle that are not divisible by p. It is known (see [3] and [7]) that the quotient Rp(n) = Tp(n)ln p is bounded above by ap = sup„>i Rp(ri) = 1 and below by J3P = in£n>\ Rp(n). The pp tend to \ with p [2], but ...
... Tp(n) = "£sp(k) is the number of binomial coefficients in the first n rows of Pascal's triangle that are not divisible by p. It is known (see [3] and [7]) that the quotient Rp(n) = Tp(n)ln p is bounded above by ap = sup„>i Rp(ri) = 1 and below by J3P = in£n>\ Rp(n). The pp tend to \ with p [2], but ...
Section 2.3: Infinite sets and cardinality
... Suppose that A and B are sets (finite or infinite). We say that A and B have the same cardinality (written |A| = |B|) if a bijective correspondence exists between A and B. In other words, A and B have the same cardinality if it’s possible to match each element of A to a different element of B in such a ...
... Suppose that A and B are sets (finite or infinite). We say that A and B have the same cardinality (written |A| = |B|) if a bijective correspondence exists between A and B. In other words, A and B have the same cardinality if it’s possible to match each element of A to a different element of B in such a ...
2.5-updated - WordPress.com
... There are uncomputable functions. We have shown that the set of Java programs is countable. Exercise 38 in the text shows that there are uncountably many different functions from a particular countably infinite set (i.e., the positive integers) to itself. Therefore (Exercise 39) there must be unco ...
... There are uncomputable functions. We have shown that the set of Java programs is countable. Exercise 38 in the text shows that there are uncountably many different functions from a particular countably infinite set (i.e., the positive integers) to itself. Therefore (Exercise 39) there must be unco ...
Polynomial
... Monomial: A number, a variable or the product of a number and one or more variables Polynomial: A monomial or a sum of monomials. Binomial: A polynomial with exactly two terms. Trinomial: A polynomial with exactly three terms. Coefficient: A numerical factor in a term of an ...
... Monomial: A number, a variable or the product of a number and one or more variables Polynomial: A monomial or a sum of monomials. Binomial: A polynomial with exactly two terms. Trinomial: A polynomial with exactly three terms. Coefficient: A numerical factor in a term of an ...
Lecture 23
... A real number R is computable if there is a (finite) program that prints out the decimal representation of R from left to right. Thus, each digit of R will eventually be output. ...
... A real number R is computable if there is a (finite) program that prints out the decimal representation of R from left to right. Thus, each digit of R will eventually be output. ...
lecture24 - Duke Computer Science
... f: AB is a bijection, and g: BC is a bijection. Then h(x) = g(f(x)) defines a function h: AC that is a bijection Hence, N, E, and Z all have the same cardinality. ...
... f: AB is a bijection, and g: BC is a bijection. Then h(x) = g(f(x)) defines a function h: AC that is a bijection Hence, N, E, and Z all have the same cardinality. ...
THE CHARNEY-DAVIS QUANTITY FOR CERTAIN GRADED POSETS
... For this reason, we call this conjecturally non-negative quantity the Charney-Davis quantity for any graded poset P . It is an easy consequence (see [4, Lemma 7.5] or [14, Proposition 1.4]) of the symmetry of W (P, t) that whenever the Neggers-Stanley Conjecture holds for P , the above Charney-Davis ...
... For this reason, we call this conjecturally non-negative quantity the Charney-Davis quantity for any graded poset P . It is an easy consequence (see [4, Lemma 7.5] or [14, Proposition 1.4]) of the symmetry of W (P, t) that whenever the Neggers-Stanley Conjecture holds for P , the above Charney-Davis ...
Term Test 2 PDF File - Department of Mathematics, University of
... B1. Show that (28) 2/5 is irrational. B3a) Must the sum of an irrational and a rational number be irrational? Prove that your answer is correct. B3b)Must an irrational number to a rational power be irrational? Prove that your answer is correct. B4. Prove that 5 1/3 + 7 1/2 is irrational. B5. Prove t ...
... B1. Show that (28) 2/5 is irrational. B3a) Must the sum of an irrational and a rational number be irrational? Prove that your answer is correct. B3b)Must an irrational number to a rational power be irrational? Prove that your answer is correct. B4. Prove that 5 1/3 + 7 1/2 is irrational. B5. Prove t ...
Bijective Correspondences and Countably Infinite Sets
... Important: if a bijective correspondence exists between two finite sets, they have the same cardinality. To emphasise: Two sets have the same cardinality if �and only if) it is possible to match each element of A to an element of B in such a way that every element of each set has exactly one “partner ...
... Important: if a bijective correspondence exists between two finite sets, they have the same cardinality. To emphasise: Two sets have the same cardinality if �and only if) it is possible to match each element of A to an element of B in such a way that every element of each set has exactly one “partner ...
15_cardinality
... The inverse of a bijective function f : A → B is the unique function f ‑1: B → A such that for any a ∈ A, f ‑1(f(a)) = a and for any b ∈ B, f(f ‑1(b)) = b A function is bijective if it has an inverse function f(a) ...
... The inverse of a bijective function f : A → B is the unique function f ‑1: B → A such that for any a ∈ A, f ‑1(f(a)) = a and for any b ∈ B, f(f ‑1(b)) = b A function is bijective if it has an inverse function f(a) ...
2.3 Infinite sets and cardinality
... from A to B that assigns different elements of B to all the elements of A and “uses” all the elements of B. A function that has these properties is called a bijection. In the case of finite sets, the second point above might seem to be overcomplicating the issue, since we can tell if two finite sets h ...
... from A to B that assigns different elements of B to all the elements of A and “uses” all the elements of B. A function that has these properties is called a bijection. In the case of finite sets, the second point above might seem to be overcomplicating the issue, since we can tell if two finite sets h ...
Section 7.5: Cardinality
... We want to define the notion of when two sets with infinitely many elements have the same size. In order to do this, we shall generalize the ideas we developed for finite sets. Recall that a one-to-one correspondence between a set X and a set Y is a function f : X → Y which is one-to-one and onto. I ...
... We want to define the notion of when two sets with infinitely many elements have the same size. In order to do this, we shall generalize the ideas we developed for finite sets. Recall that a one-to-one correspondence between a set X and a set Y is a function f : X → Y which is one-to-one and onto. I ...
+ (3 12 5 1)
... When you count the number of possible permutations of a set of elements, order is important. As a final topic in this section, you will look at a method of selecting subsets of a larger set in which order is not important. Such subsets are called combinations of n elements taken r at a time. Example ...
... When you count the number of possible permutations of a set of elements, order is important. As a final topic in this section, you will look at a method of selecting subsets of a larger set in which order is not important. Such subsets are called combinations of n elements taken r at a time. Example ...
Generating Functions
... Here Ak is a set with k elements, and Partn (Ak ) consists of all set partitions of Ak into n blocks, that is, into all decompositions of Ak into n blocks, disregarding order. Then akj is the combinatorial coefficient associated with a block in the set partition of A of size kj . So a complicated op ...
... Here Ak is a set with k elements, and Partn (Ak ) consists of all set partitions of Ak into n blocks, that is, into all decompositions of Ak into n blocks, disregarding order. Then akj is the combinatorial coefficient associated with a block in the set partition of A of size kj . So a complicated op ...
countably infinite
... subset of the natural numbers N, then the set is called countable. If |A| = |N|, the set A is countably infinite. The (transfinite) cardinal number of the set N is aleph null = ﭏ0. If a set is not countable we say it is uncountable. P. 1 ...
... subset of the natural numbers N, then the set is called countable. If |A| = |N|, the set A is countably infinite. The (transfinite) cardinal number of the set N is aleph null = ﭏ0. If a set is not countable we say it is uncountable. P. 1 ...
6.5 B Worksheet - Militant Grammarian
... compartment must be 2 meters longer than it is wide and its depth must be 1 meter less than its width. The volume of the compartment must be ...
... compartment must be 2 meters longer than it is wide and its depth must be 1 meter less than its width. The volume of the compartment must be ...
Practice B
... compartment must be 2 meters longer than it is wide and its depth must be 1 meter less than its width. The volume of the compartment must be ...
... compartment must be 2 meters longer than it is wide and its depth must be 1 meter less than its width. The volume of the compartment must be ...