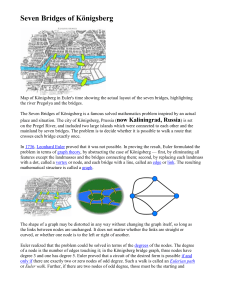
Maths NC Stage 9 skills
... Solve linear inequalities in one variable Represent the solution set to an inequality on a number line Solve, in simple cases, two linear simultaneous equations in two variables algebraically Derive an equation (or two simultaneous equations), solve the equation (s) and interpret the solution Find a ...
... Solve linear inequalities in one variable Represent the solution set to an inequality on a number line Solve, in simple cases, two linear simultaneous equations in two variables algebraically Derive an equation (or two simultaneous equations), solve the equation (s) and interpret the solution Find a ...
Pre-Calculus H
... Solution: We suppose that the answer is some number. We don’t know what the answer is, so we’ll call it a bi , since that can be any number you could think of. In other words, we need to find a and b such that: 4 3i a bi Now algebra happens. Square both sides and get 4 3i a 2 b2 2abi ...
... Solution: We suppose that the answer is some number. We don’t know what the answer is, so we’ll call it a bi , since that can be any number you could think of. In other words, we need to find a and b such that: 4 3i a bi Now algebra happens. Square both sides and get 4 3i a 2 b2 2abi ...
STEP Support Programme Assignment 9 Warm-up
... Euclid’s Proposition 5 says that the base angles of an isosceles triangle are equal. Euclid’s proof was a bit harder than the one suggested in question 1(i), because he had not by that point (i.e. in propositions 1 to 4) shown that two triangles with corresponding sides of the same length are congru ...
... Euclid’s Proposition 5 says that the base angles of an isosceles triangle are equal. Euclid’s proof was a bit harder than the one suggested in question 1(i), because he had not by that point (i.e. in propositions 1 to 4) shown that two triangles with corresponding sides of the same length are congru ...
Black Assessment - Challenge by Choice with Tiered Instruction and
... 8. On the planet of Creon, every creature is exactly the same height (80 cm), but no creature is the same weight, though the heaviest creature is 100 kg. a. Graph the relationship between x, the height of each creature, and y, each creature’s weight. (1 pt) b. Write an equation for this graph? ...
... 8. On the planet of Creon, every creature is exactly the same height (80 cm), but no creature is the same weight, though the heaviest creature is 100 kg. a. Graph the relationship between x, the height of each creature, and y, each creature’s weight. (1 pt) b. Write an equation for this graph? ...
Unit 5: Geometry - Fairfield Public Schools Math Wikispace
... Reinforce strategies that help your child think flexibly about numbers. Encourage them to think about how to compose, decompose, and group numbers to find efficient ways to solve problems. Encourage your child to explain her/his thinking as he/she solves problems. ...
... Reinforce strategies that help your child think flexibly about numbers. Encourage them to think about how to compose, decompose, and group numbers to find efficient ways to solve problems. Encourage your child to explain her/his thinking as he/she solves problems. ...
A new class of graphs that satisfies the Chen
... graph induces a metric space on its vertex set, where the distance between two vertices u and v is defined as the length of a shortest path linking u and v. Such metric spaces are called graph metrics and are the subject of this paper. The best known lower bound on the number of lines in a graph met ...
... graph induces a metric space on its vertex set, where the distance between two vertices u and v is defined as the length of a shortest path linking u and v. Such metric spaces are called graph metrics and are the subject of this paper. The best known lower bound on the number of lines in a graph met ...
step assignment 9 - March
... Euclid’s Proposition 5, which is proved in part (i) of the warm-up above, says that the base angles of an isosceles triangle are equal. Euclid’s proof was a bit harder than the one suggested in part (i) above, because he had not yet (i.e. in propositions 1 to 4) shown that two triangles with corresp ...
... Euclid’s Proposition 5, which is proved in part (i) of the warm-up above, says that the base angles of an isosceles triangle are equal. Euclid’s proof was a bit harder than the one suggested in part (i) above, because he had not yet (i.e. in propositions 1 to 4) shown that two triangles with corresp ...
Year 9 Maths Assessment Criteria
... Calculate with standard form Use the form y = mx + c to A x 10n, where 1 ≤ A < 10 and identify parallel lines n is an integer ...
... Calculate with standard form Use the form y = mx + c to A x 10n, where 1 ≤ A < 10 and identify parallel lines n is an integer ...
7th Grade Common Core Appendix to Math Curriculum
... Below, we have matched up the new Core Curriculum Standards with our own New York State math standards for reference. On the left are the Common Core Standards in the order that they have been p ...
... Below, we have matched up the new Core Curriculum Standards with our own New York State math standards for reference. On the left are the Common Core Standards in the order that they have been p ...
I.1 Connected Components
... Connectivity. In a simple graph, a path from u ∈ V to v ∈ V can be described by a sequence of vertices, u = u0 , u1 , u2 , . . . , uk = v, where we have an edge from ui to ui+1 for each 0 ≤ i ≤ k − 1. Vertices can repeat allowing the path to cross itself or fold onto itself. Definition A. A simple g ...
... Connectivity. In a simple graph, a path from u ∈ V to v ∈ V can be described by a sequence of vertices, u = u0 , u1 , u2 , . . . , uk = v, where we have an edge from ui to ui+1 for each 0 ≤ i ≤ k − 1. Vertices can repeat allowing the path to cross itself or fold onto itself. Definition A. A simple g ...
Italo Jose Dejter

Italo Jose Dejter (Bahia Blanca, 1939) is an Argentine-born American mathematician of Bessarabian Jewish descent. He is a professor at the University of Puerto Rico (UPRRP) since 1984 and has conducted research in mathematics, particularly in areas that include algebraic topology, differential topology, graph theory, coding theory and design theory.He has an Erdos number of 2 since 1993.Dejter completed the Licentiate degree in Mathematics from University of Buenos Aires in 1967, and the Ph.D. degree in Mathematics from Rutgers University in 1975 under the supervision of Ted Petrie. He was a professor atFederal University of Santa Catarina, Brazil, from 1977 to 1984. Dejter has been a visiting scholar at a number of research institutions, including University of São Paulo,Instituto Nacional de Matemática Pura e Aplicada, Federal University of Rio Grande do Sul,University of Cambridge,National Autonomous University of Mexico, Simon Fraser University, University of Victoria, New York University, University of Illinois at Urbana–Champaign, McMaster University,DIMACS, Autonomous University of Barcelona, Technical University of Denmark, Auburn University, Polytechnic University of Catalonia, Technical University of Madrid, Charles University, Ottawa University, Simón Bolívar University, etc. The sections below describe the relevance of Dejter's work in the research areas mentioned in the first paragraph above, or in the box to the right.