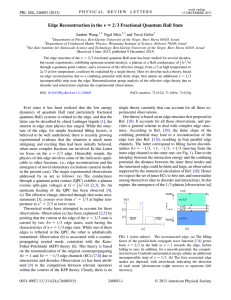
waves
... •Best guess: The particle is in the center, x = L/2 •But there is an error x on this amount Exact numbers for x: •It is no greater than L/2 •Particle in a box: 0.181L •It is certainly bigger than 0 •Uniform distribution: 0.289L •Carlson’s rule: use x = L/4 •This rule can be applied in the time do ...
... •Best guess: The particle is in the center, x = L/2 •But there is an error x on this amount Exact numbers for x: •It is no greater than L/2 •Particle in a box: 0.181L •It is certainly bigger than 0 •Uniform distribution: 0.289L •Carlson’s rule: use x = L/4 •This rule can be applied in the time do ...
Qubit metrology for building a fault-tolerant quantum
... their logic interactions must have errors below a threshold: scaling up with more and more qubits then brings the net error probability down to appropriate levels needed for running complex algorithms. Reducing error requires solving problems in physics, control, materials and fabrication, which dif ...
... their logic interactions must have errors below a threshold: scaling up with more and more qubits then brings the net error probability down to appropriate levels needed for running complex algorithms. Reducing error requires solving problems in physics, control, materials and fabrication, which dif ...
Polynomial-Time Algorithms for Prime Factorization and Discrete
... the same polynomial growth in precision does not appear to confer extra computing power to classical mechanics, although allowing exponential growth in precision may [Hartmanis and Simon, 1974; Vergis, Steiglitz, and Dickinson, 1986]. As far as we know, the precision possible in quantum state manipu ...
... the same polynomial growth in precision does not appear to confer extra computing power to classical mechanics, although allowing exponential growth in precision may [Hartmanis and Simon, 1974; Vergis, Steiglitz, and Dickinson, 1986]. As far as we know, the precision possible in quantum state manipu ...
Solving Momentum Problems
... is moving in the direction opposite that defined as positive will have a negative momentum. You can also break a momentum vector into components or resolve momentum vectors into a single resultant. Momentum is a conserved quantity. The momentum of a system will not change unless an outside impulse i ...
... is moving in the direction opposite that defined as positive will have a negative momentum. You can also break a momentum vector into components or resolve momentum vectors into a single resultant. Momentum is a conserved quantity. The momentum of a system will not change unless an outside impulse i ...
Aspects of the Quantum Hall Effect
... one edge to the other, thereby making it possible to do work against a potential gradient in a direction transverse to the electric current induced by the changing flux. This gives rise to a Hall conductance quantized at integer values. These arguments hold quite generally – immune to details of the ...
... one edge to the other, thereby making it possible to do work against a potential gradient in a direction transverse to the electric current induced by the changing flux. This gives rise to a Hall conductance quantized at integer values. These arguments hold quite generally – immune to details of the ...
Generating random density matrices
... are distributed according to the unique, unitarily invariant, Haar measure dµV on U (N ). Taking this assumption as granted, the measure in the space of density matrices will be determined by the first factor dν describing the joint distribution of eigenvalues P (λ1 , . . . , λN ). In quantum theory ...
... are distributed according to the unique, unitarily invariant, Haar measure dµV on U (N ). Taking this assumption as granted, the measure in the space of density matrices will be determined by the first factor dν describing the joint distribution of eigenvalues P (λ1 , . . . , λN ). In quantum theory ...