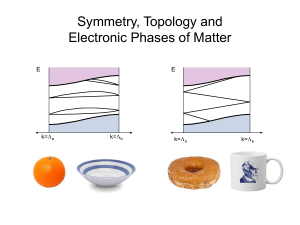
Symmetry, Topology and Electronic Phases of Matter
... = Boundary Invariant - Chern number n = # chiral edge modes ...
... = Boundary Invariant - Chern number n = # chiral edge modes ...
Electronic Structure of Superheavy Atoms. Revisited.
... EF (r), where F are doublets (with components f (r) and g (r)) from the Hilbert space L2 (R+ ) = L2 (R+ )⊕L2 (R+ ) and ĥ (Z, j, ζ) are some s.a. radial Hamiltonians acting on the doublets F (r) by radial differential operations ȟ (Z, j, ζ) = −iσ2 dr +ζ(j +1/2)r−1 σ1 −qr−1 +mσ3 . (2) On basis of th ...
... EF (r), where F are doublets (with components f (r) and g (r)) from the Hilbert space L2 (R+ ) = L2 (R+ )⊕L2 (R+ ) and ĥ (Z, j, ζ) are some s.a. radial Hamiltonians acting on the doublets F (r) by radial differential operations ȟ (Z, j, ζ) = −iσ2 dr +ζ(j +1/2)r−1 σ1 −qr−1 +mσ3 . (2) On basis of th ...
Research Paper
... Quantum Computer 7 is relatively in check. Everyday hundreds of thousands of sophisticated attacks probe the United States’ infrastructure, but for the most part the Department of Homeland Security, the Pentagon, and the new US Cyber Command have managed to defeat and even retaliate to cyber attack ...
... Quantum Computer 7 is relatively in check. Everyday hundreds of thousands of sophisticated attacks probe the United States’ infrastructure, but for the most part the Department of Homeland Security, the Pentagon, and the new US Cyber Command have managed to defeat and even retaliate to cyber attack ...
Rotational Motion and Torque
... • When objects are not rigidly attached to the rotational axis, an outside force must push / pull on the object to keep it spinning. Gravity is such a force that acts on the mass of an object by the mutual attraction between two objects due to the mass of each object and the distance between them. ...
... • When objects are not rigidly attached to the rotational axis, an outside force must push / pull on the object to keep it spinning. Gravity is such a force that acts on the mass of an object by the mutual attraction between two objects due to the mass of each object and the distance between them. ...
IOSR Journal of Applied Physics (IOSR-JAP)
... application of Einstein’s field equations, with some success. Recently, some work on gauge symmetries in spinfoam gravity has been reported [10]. An interesting work on spin and quantization of gravitational space has also been reported [11]. Recently, there have been a lot of research activities to ...
... application of Einstein’s field equations, with some success. Recently, some work on gauge symmetries in spinfoam gravity has been reported [10]. An interesting work on spin and quantization of gravitational space has also been reported [11]. Recently, there have been a lot of research activities to ...
CHM 4412 Physical Chemistry II - University of Illinois at
... equation – the equation of motion of quantum mechanics and “the whole of chemistry.”* The time-independent Schrödinger equation parallels Hamilton’s equation in classical mechanics and physically represents conservation of energy. It incorporates the wave-particle duality and quantization of energy. ...
... equation – the equation of motion of quantum mechanics and “the whole of chemistry.”* The time-independent Schrödinger equation parallels Hamilton’s equation in classical mechanics and physically represents conservation of energy. It incorporates the wave-particle duality and quantization of energy. ...
Here
... mapped to the Gauss-Manin connection of the family Yb . The latter is the flat connection induced by the continuous family of lattices H ∗ (Y, Z) ⊂ H ∗ (Y, C). Given a family of symplectictomorphic spaces such as Yb , one can often produce a ‘symplectic connection’ which associates to a path in the ...
... mapped to the Gauss-Manin connection of the family Yb . The latter is the flat connection induced by the continuous family of lattices H ∗ (Y, Z) ⊂ H ∗ (Y, C). Given a family of symplectictomorphic spaces such as Yb , one can often produce a ‘symplectic connection’ which associates to a path in the ...
What is density operator?
... for every observable (physical quantity) O q except those that are proportional to the identity operator. In orther words, for any given state in the Hilbert space there are plenty of questions one can ask to which there is no definite answer! Contrast this to the classical situation – if you know t ...
... for every observable (physical quantity) O q except those that are proportional to the identity operator. In orther words, for any given state in the Hilbert space there are plenty of questions one can ask to which there is no definite answer! Contrast this to the classical situation – if you know t ...
- Philsci
... be the case. The particle labels might be outright fictions. In fact, given that the labeled tensor product Hilbert Space formalism of many-particle quantum mechanics allows, in virtue of the indices, non-symmetric states that do not occur in nature, it would appear that the labels are not just otio ...
... be the case. The particle labels might be outright fictions. In fact, given that the labeled tensor product Hilbert Space formalism of many-particle quantum mechanics allows, in virtue of the indices, non-symmetric states that do not occur in nature, it would appear that the labels are not just otio ...
An introduction to quantum probability, quantum mechanics, and
... measured values have probability distributions. Although we will discuss the vector-state model, we will emphasize the non-commutative probability model from operator algebras. In this model, a system can be fully quantum, or fully classical, or things in between. The fully quantum case corresponds ...
... measured values have probability distributions. Although we will discuss the vector-state model, we will emphasize the non-commutative probability model from operator algebras. In this model, a system can be fully quantum, or fully classical, or things in between. The fully quantum case corresponds ...
Computation of hadronic two-point functions in Lattice QCD
... where X = (x, α, i), Y = (y, β, j) are multi-indices: we can obtain a quark two-point function on a fixed gauge field background (= quark propagator) by inverting the Dirac matrix. On the lattice there are NS3 NT distinct sites, e.g., 323 64 = 221 ≈ 2 · 106 . The fermion matrix A has (12NS3 NT )2 co ...
... where X = (x, α, i), Y = (y, β, j) are multi-indices: we can obtain a quark two-point function on a fixed gauge field background (= quark propagator) by inverting the Dirac matrix. On the lattice there are NS3 NT distinct sites, e.g., 323 64 = 221 ≈ 2 · 106 . The fermion matrix A has (12NS3 NT )2 co ...
On the Relation between the Spin and the Magnetic Moment of the
... which vanishes if and only if the charge to mass ratio is the same for the up and down quarks. So the oscillation occurs, if and only if the charge to mass ratio is different for the up and down quarks, or equivalently if and only if the magnetic moment is not parallel to the spin. ...
... which vanishes if and only if the charge to mass ratio is the same for the up and down quarks. So the oscillation occurs, if and only if the charge to mass ratio is different for the up and down quarks, or equivalently if and only if the magnetic moment is not parallel to the spin. ...























