Hamiltonian Mechanics and Symplectic Geometry
... is determined by six numbers, the coordinates of the position (q1 , q2 , q3 ) and the momentum (p1 , p2 , p3 ). The space R6 of positions and momenta is called “phase space.” The time evolution of the system is determined by a single function of these six variables called the Hamiltonian and denoted ...
... is determined by six numbers, the coordinates of the position (q1 , q2 , q3 ) and the momentum (p1 , p2 , p3 ). The space R6 of positions and momenta is called “phase space.” The time evolution of the system is determined by a single function of these six variables called the Hamiltonian and denoted ...
S. Mayboroda:
... S. Mayboroda: Localization of Eigenfunctions The property of the localization of the eigenfunctions in rough domains or rough materials permeates acoustics, quantum physics, elasticity, to name just a few. Localization on fractal domains was used for noise abatement walls which up to date hold world ...
... S. Mayboroda: Localization of Eigenfunctions The property of the localization of the eigenfunctions in rough domains or rough materials permeates acoustics, quantum physics, elasticity, to name just a few. Localization on fractal domains was used for noise abatement walls which up to date hold world ...
1 The Time-Dependent and Time-Independent Schrödinger Equations
... Do not confuse this with an eigenvalue equation: the right hand side has an operator Ê, not a scalar value E. For time-independent problems the Hamiltonian operator does not explicitly depend on the time t, i.e, Ĥ ≡ Ĥ(x, y, z). We must have the probability density ΨΨ∗ independent of time. This re ...
... Do not confuse this with an eigenvalue equation: the right hand side has an operator Ê, not a scalar value E. For time-independent problems the Hamiltonian operator does not explicitly depend on the time t, i.e, Ĥ ≡ Ĥ(x, y, z). We must have the probability density ΨΨ∗ independent of time. This re ...
Lecture 29 - USU physics
... variance in Eq. (6a). Finally, the square root of the variance is the standard deviation ∆x . This whole process is then repeated, except this time a series of momentum measurements is made, allowing one to find ∆p x . What we want to do here, however, is use the theory of quantum mechanics to calcu ...
... variance in Eq. (6a). Finally, the square root of the variance is the standard deviation ∆x . This whole process is then repeated, except this time a series of momentum measurements is made, allowing one to find ∆p x . What we want to do here, however, is use the theory of quantum mechanics to calcu ...
Chapter 7: Quantum Mechanical Model of Atom
... • Erwin Schrödinger - proposed quantum mechanical model of atom, which focuses on wavelike properties of electrons. ...
... • Erwin Schrödinger - proposed quantum mechanical model of atom, which focuses on wavelike properties of electrons. ...
4 Canonical Quantization
... In particular, two operators that do not commute with each other cannot be diagonalized simultaneously. Hence it is not possible to measure simultaneously two non-commuting observables with arbitrary precision in the same physical state. This is the the Uncertainty Principle. By following this presc ...
... In particular, two operators that do not commute with each other cannot be diagonalized simultaneously. Hence it is not possible to measure simultaneously two non-commuting observables with arbitrary precision in the same physical state. This is the the Uncertainty Principle. By following this presc ...
Self-reference Systems. ppt
... Let us define necessary lifetime story of the quantum particle; Particle meditans lives in, say, Euclid space with no field and collidens is guided (by some other particle) along geodesics of the actual field Elementary idem is <...|action of the field described as interaction of two single particle ...
... Let us define necessary lifetime story of the quantum particle; Particle meditans lives in, say, Euclid space with no field and collidens is guided (by some other particle) along geodesics of the actual field Elementary idem is <...|action of the field described as interaction of two single particle ...
6.1.2. Number Representation: States
... Consider a set of complete, orthonormal 1-particle (1-P) basis. For the sake of clarity, we shall assume the quantum numbers to be discrete. (Results for the continuous case can be obtained by some limiting procedure). To begin, we arrange the 1-P states by some rule into a unique sequence 0,1,2 ...
... Consider a set of complete, orthonormal 1-particle (1-P) basis. For the sake of clarity, we shall assume the quantum numbers to be discrete. (Results for the continuous case can be obtained by some limiting procedure). To begin, we arrange the 1-P states by some rule into a unique sequence 0,1,2 ...
ij - Scientific Research Publishing
... Review of the irreversibility problem in modern physics with new researches is given. Some characteristics of the Markov chains are specified and the important property of monotonicity of a probability is formulated. Using one thin inequality, the behavior of relative entropy in the classical case i ...
... Review of the irreversibility problem in modern physics with new researches is given. Some characteristics of the Markov chains are specified and the important property of monotonicity of a probability is formulated. Using one thin inequality, the behavior of relative entropy in the classical case i ...
Quantum Theory of Condensed Matter: Problem Set 1 Qu.1
... interacting many-body problem, the transverse field Ising model in one space dimension. The solution uses two operator transformations – the Jordan-Wigner transformation and the Bogoluibov transformation – which are useful in many other contexts. Consider a one-dimensional lattice with site-label m. ...
... interacting many-body problem, the transverse field Ising model in one space dimension. The solution uses two operator transformations – the Jordan-Wigner transformation and the Bogoluibov transformation – which are useful in many other contexts. Consider a one-dimensional lattice with site-label m. ...
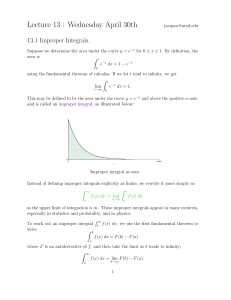
Lecture 13 : Wednesday April 30th
... 12.3 Other improper integrals In all the integrals so far, the functions we have dealt with are continuous on the range of integration. Another type of improper integral arises when the integrand is discontinuous over the range of integration, due to the presence of vertical asymptotes. For example, ...
... 12.3 Other improper integrals In all the integrals so far, the functions we have dealt with are continuous on the range of integration. Another type of improper integral arises when the integrand is discontinuous over the range of integration, due to the presence of vertical asymptotes. For example, ...
Showing-up the Extra-Dimensions of Electron
... • Following Zeldovich-1968 [13] we assume, qualitatively, that the fluctuations of a physical vacuum as a global effect of the averaged cosmological constant would be a mechanism for rolling the transverse time axes. • Defining the wave (1) polarized circularly along the axis thus its evolution keep ...
... • Following Zeldovich-1968 [13] we assume, qualitatively, that the fluctuations of a physical vacuum as a global effect of the averaged cosmological constant would be a mechanism for rolling the transverse time axes. • Defining the wave (1) polarized circularly along the axis thus its evolution keep ...
PHYS13071 Assessment 2012
... Bohr and Copenhagen institute Heisenberg’s matrix mechanics Schrodinger’s wave mechanics Solvay conferences and the Bohr-Einstein debate ...
... Bohr and Copenhagen institute Heisenberg’s matrix mechanics Schrodinger’s wave mechanics Solvay conferences and the Bohr-Einstein debate ...
down
... 2.7 Eigenfunctions of Q.M. operator form a complete set completeness in 3-dimensional vector space : Any vector in 3-dimensional can be represented by linear combination of vector x, y, and z Similar, completeness in functional space : Wave function can be expanded in the eigenfunctions of any Q.M. ...
... 2.7 Eigenfunctions of Q.M. operator form a complete set completeness in 3-dimensional vector space : Any vector in 3-dimensional can be represented by linear combination of vector x, y, and z Similar, completeness in functional space : Wave function can be expanded in the eigenfunctions of any Q.M. ...
Presentation - University of Colorado Boulder
... Use superposition to calculate 2n values of function simultaneously and do not read out the result until a useful outout is expected with reasonably high probability. Use entanglement: measurement of states can be highly correlated ...
... Use superposition to calculate 2n values of function simultaneously and do not read out the result until a useful outout is expected with reasonably high probability. Use entanglement: measurement of states can be highly correlated ...
Relation Between Schrödinger and Polymer Quantum Mechanics
... Is there a price? Yes! The quantum theory becomes discontinuous. This means that for a system with p̂ and q̂ as fundamental coordinates, one of them becomes ill-defined. But if the Hamiltonian is of the form H = p2 + V (q), we can not define it on the Kinematical Hilbert space H. Can we do something ...
... Is there a price? Yes! The quantum theory becomes discontinuous. This means that for a system with p̂ and q̂ as fundamental coordinates, one of them becomes ill-defined. But if the Hamiltonian is of the form H = p2 + V (q), we can not define it on the Kinematical Hilbert space H. Can we do something ...