Download LECTURE 18

PHYSICS 420
SPRING 2006
Dennis Papadopoulos
LECTURE 18
EXPECTATION VALUES
QUANTUM OPERATORS
•We can find allowed wave-functions.
•We can find allowed energy levels by plugging those wavefunctions into
the Schrodinger equation and solving for the energy.
•We know that the particle’s position cannot be determined precisely, but
that the probability of a particle being found at a particular point can be
calculated from the wave-function.
•Okay, we can’t calculate the position (or other position dependent
variables) precisely but given a large number of events, can we predict
what the average value will be? (If you roll a dice once, you can only
guess that the number rolled will be between 1 and 6, but if you roll a
dice many times, you can say with certainty that the fraction of times you
rolled a three will converge on 1 in 6…)
SHARP AND FUZZY
OBSERVABLES
• Two types of measurable quantities
associated with Y or y
– Sharp: e.g. Energy for stationary states. Every
measurement performed gives the same value
controlled by the quantum labeling of the wave n.
– Fuzzy: e.g. position or momentum. A partiple
described by y can have occupy different places
and have different momentum, with a probability
given by yy*. Predictions for y can be tested by
making repeated measurement of the quantity.
If you roll a dice 600 times, you can
average the results as follows:
1  2  4  6  5  5  3  4  ...
600
Alternatively, you can count the number of
times you rolled a particular number and
weight each number by the the number of
times it was rolled, divided by the total
number of rolls of the dice:
99
97
104
(1) 
(2) 
(3)  ...
600
600
600
After a large number of rolls, these ratios
converge on the probability for rolling a
particular value, and the average value
can then be written:
x   xPx
This works any time you have discreet values.
What do you do if you have a continuous variable,
such as the probability density for you particle?




2
 x   xPx dx   x Y ( x, t ) dx
It becomes an integral….
2.5  3.7  1.4  ....  5.3
 5.46
18
1.4(1/18)  2.5(1/18)  ...  5.4(3 /18)  6.2(2 /18)  ...  8.8(1/18)  5.46
x
x   xPx
Expectation, value

x 


x Y ( x, t ) dx
2
Table 6-1, p. 217
The expectation value can be interpreted as the average value of x that we
would expect to obtain from a large number of measurements. Alternatively it
could be viewed as the average value of position for a large number of
particles which are described by the same wave-function.
We have calculated the expectation value for the position x, but this can be
extended to any function of positions, f(x).
For example, if the potential is a function of x, then:

U   U ( x) Y( x, t ) dx

2
UNCERTAINTY AND STADARD
DEVIATION
Standard Deviation

x 
 x Y ( x, t )
2
dx
N



f 

f ( x) Y ( x, t ) dx


1
N
N
 
2

x 2 Y ( x, t ) dx
2
x )2
i
2

x2 
 (x 
 (x )
1
N
 x2  x

x 
2
i
N
 2 x ( ( xi ) / N )  x
1
2
N
 (1/ N ) 
x2  2 x x  x
1
2
x2  x
x2  x
2
2
If all xi the same =0 and observable is sharp. Otherwise is fuzzy subject to the UP.
2

QUANTUM OPERATORS
Found how to predict <x> and its position uncertainty x. Same for <U>.
How about p or KE?
We could do it if p was a function of position, i.e. p=p(x) was known.
however in QM we cannot measure simultaneously x and p. Of course we
can do it in classical physics since all observables are sharp and the
uncertainty is related to measurement errors. In QM there is no path that
connects p and x.
Need different approach. Identify <p> with <p>=m (d<x>/dt. Cannot be
derived but guessed since it reduces to the correct classical limit.
p m
d x
dt
 SE   

p 
m
d 
{ x[Y ( x, t )Y * ( x, t )]dx}
dt 
h Y ( x, t )
dx
x
 Y ( x, t )( i )
*

Momentum operator
h 
i x
expression for
kinetic energy
p2
KE 
;
2m
the potential
kinetic plus potential
energy gives the total
energy
p  hk
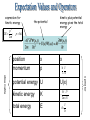
position
momentum
x
p
x
potential energy U
U(x)
kinetic energy
K
h 2 2

2m x 2
total energy
E
ih

t
operator
observable
h 
i x
In general to calculate the expectation value of some observable quantity:
Q   Y* QYdx


We’ve learned how to calculate the observable of a value that is simply a function of x:
U   Y U Ydx   Y U ( x)Ydx   U ( x) Y dx


*


*

2

But in general, the operator “operates on” the wave-function and the
exact order of the expression becomes important:
 h 2 2Y 
K   Y  K Ydx   Y  
dx
2 


 2m x 

*

*
Table 6-2, p. 222