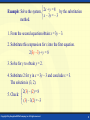Download Solving Systems of Linear Equations

Digital Lesson
Solving Systems of
Linear Equations
A set of linear equations in two variables is called
a system of linear equations.
 3x + 2y = 14

 2x + 5y = 3
A solution of such a system is an ordered pair which is a solution
of each equation in the system.
Example: The ordered pair (4, 1) is a solution of the system since
3(4) + 2(1) = 14 and 2(4) – 5(1) = 3.
Example: The ordered pair (0, 7) is not a solution of the system
since
3(0) + 2(7) = 14 but 2(0) – 5(7) = – 35, not 3.
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
2
Methods to solve linear systems
• Graphing
• substitution method
• Addition method (elimination method)
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
3
Systems of linear equations in two variables have either
no solutions, one solution, or infinitely many solutions.
y
y
y
x
unique solution
x
infinitely many
solutions
x
no solutions
A system of equations with at least one solution is consistent.
A system with no solutions is inconsistent.
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
4
 x – y = –1
To solve the system 
by the graphing method,
 2x + y = 4
graph both equations and determine where the graphs intersect.
y
3
(1, 2)
x – y = –1
1
x
2x + y = 4
The ordered pair (1, 2) is the unique solution.
The system is consistent since it has solutions.
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
5
x – 2y = – 4

Example: Solve the system 
by the graphing
 3x – 6y = 6
method.
y
3
x – 2y = – 4
x
2
3x – 6y = 6
The lines are parallel and have no point of intersection.
The system has no solutions and is inconsistent.
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
6
 x – 2y = – 4
Example: Solve the system 
by the graphing
3x – 6y = – 12

method.
y
3
2y == –– 12
4
3xx –– 6y
x
2
The graphs of the two equations are the same line and the
intersection points are all the points on this line.
The system has infinitely many solutions.
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
7
To solve a system by the substitution method:
1. Select an equation and solve for one variable in
terms of the other.
2. Substitute the expression resulting from Step 1 into
the other equation to produce an equation in one
variable.
3. Solve the equation produced in Step 2.
4. Substitute the value for the variable obtained in
Step 3 into the expression obtained in Step 2.
5. Check the solution.
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
8

Example: Solve the system  2x + y = 8 by the substitution
x – 3y = – 3

method.
1. From the second equation obtain x = 3y – 3.
2. Substitute this expression for x into the first equation.
2(3y –3) + y = 8
3. Solve for y to obtain y = 2.
4. Substitute 2 for y in x = 3y – 3 and conclude x = 3.
The solution is (3, 2).
2(3) – (2) = 8
5. Check: 

 (3) – 3(2) = –3
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
9
 2x – y = 10
Example: Solve the system 
by the substitution
4x – 2y = 8
method.
1. From the first equation obtain y = 2x – 10.
2. Substitute 2x – 10 for y into the second equation to produce
4x – 2(2x – 10) = 8.
3. Attempt to solve for x.
4x – 2(2x – 10) = 8
4x – 4x + 20 = 8
20 = 8 False statement
Because there are no values of x and y for which 20 equals 8, this
system has no solutions.
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
10
To solve a system by the addition (or elimination) method:
1. Multiply either or both equations by nonzero
constants to obtain opposite coefficients for one of
the variables in the system.
2. Add the equations to produce an equation in
one variable. Solve this equation.
3. Substitute the value of the variable found in Step 2
into either of the original equations to obtain another
equation in one variable. Solve this equation.
4. Check the solution.
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
11
Example: Solve the system 5x + 2y = 11 by the addition
3x + 4y = 15
method.

1. Multiply the first equation by –2 to
make the coefficients of y opposites.
– 10 x – 4y = – 22
 3x + 4y = 15

2. Add the equations to obtain – 7x = –7.
Therefore x = 1.
3. Use back substitution to substitute 1 for x in the first equation to
produce
5(1) + 2y = 11
2y = 6
Therefore y = 3. The solution is (1, 3).
 5(1) + 2(3) = 11
4. Check: 
 3(1) + 4(3) = 15
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
12
 8x + 8y = 1920
Example continued: Solve the system 
 12x – 12y = 1920
using the addition method.
1. Multiply the first equation by 3 and the second equation by 2.
 3(8x + 8y) = 3(1920)

 2(12x – 12y) = 2(1920)
 24x + 24y = 5760

 24x – 24y = 3840
2. Add the equations to obtain 48 x = 9600. Therefore x = 200.
3. Substitute 200 for x in the first equation.
y = 40
8(200) + 8y = 1920
Copyright © by Houghton Mifflin Company, Inc. All rights reserved.
13