Download polypro P1

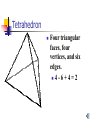
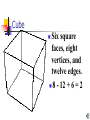
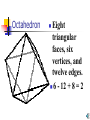
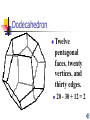
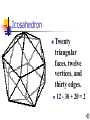
Polypro
Presentation by: Kerry Daugherty, Alison
Divens, Ryan Warfel, Jennifer Watters, Ashlie
Hill, Matt Winner, Lindsey Camarata, Amanda
Hauf
Polyhedra



Polyhedra are three-dimensional solids which
consist of a collection of polygons, usually
joined at their polyhedron edges.
The word “polyhedra” is derived from the
Greek word poly (many) plus the IndoEuropean word hedron (seat).
The plural of polyhedron is "polyhedra" (or
sometimes "polyhedrons").
Euler’s polyhedral formula



A formula relating the number of
polyhedron vertices V, faces F, and
polyhedron edges E of a simply
connected polyhedra.
Discovered independently by Euler
(1752) .
Formula states: F+V-E=2
There are 5 types of regular
polyhedra:
• Tetrahedron
• Cube
• Octahedron
• Dodecahedron
• Icosahedron
Tetrahedron

Four
triangular
`
faces, four
vertices, and six
edges.
 4 - 6 + 4 = 2
Cube
Six square
faces, eight
vertices, and
twelve edges.
 8 - 12 + 6 = 2

Octahedron
Eight
triangular
faces, six
vertices, and
twelve edges.
 6 - 12 + 8 = 2

Dodecahedron

Twelve
pentagonal
faces, twenty
vertices, and
thirty edges.

20 - 30 + 12 = 2
Icosahedron

Twenty
triangular
faces, twelve
vertices, and
thirty edges.

12 - 30 + 20 = 2
Why are there only 5 regular
polyhedra?


Each vertex has at least three faces that come
together, because if only two came together
they would collapse against one another and we
would not get a solid.
The sum of the interior angles of the faces
meeting at each vertex must be less than 360°,
for otherwise they would not all fit together.
Examples

The interior angles
of the regular
pentagon are 108°,
so we can fit only
three together at a
vertex, giving us the
dodecahedron.
The
interior angles
of a hexagon are
120°, so the angles
sum up to precisely
360°, and therefore
they lie flat, just
like four squares,
and do not form a
solid.
The history of the polyhedra



The Greek philosopher Plato followed
earlier philosophers in assigning the
polyhedra to atoms of nature.
Plato also assigned polyhedra properties.
Johannes Kepler used polyhedra to
explain planetary motion
Kepler’s theory on polyhedra



Johannes Kepler
believed that polyhedra
were related to the
planets.
Believed that planets
moved in circles around
the sun.
Theory later proved
wrong by Sir Isaac
Newton.
Using Polypro

Polypro is a software program that can
assist in exploring the 5 Platonic solids,
along with pyramids and prisms.
Polypro

Polypro can be used to view and
construct the 5 Platonic Solids, along
with prisms and pyramids
Prisms

A prism is a polyhedron, with two
parallel faces called bases. The
other faces are always
parallelograms. The prism is
named by the shape of its base.
Pyramids

A polyhedron is a pyramid if it has
3 or more triangular faces sharing
a common vertex. The base of a
pyramid may be any polygon.
How to start constructing
polyhedra

Create a net
Finishing your polyhedra


Connect all of the
pieces together to
form a solid.
You can now
perform your own
hands-on
investigation of
polyhedra
properties.
Constructing the Polyhedron

Children can
investigate
polyhedrons by
the hands-on
activities
Teaching Polyhedrons and Polypro
Elementary ( 4th and 5th grade)
students may have difficulties
understanding Polypro.
They can, however, benefit from
the hands-on activities of
constructing their own
polyhedron.

Teaching Polyhedrons and Polypro




Middle School students are able to use and
understand Polypro.
They will be able to investigate the program with
guidance.
They can draw and create nets for the objects and
build a polyhedron.
The teacher can ask the children to be creative in
their construction of their polyhedron. For example:
Children can create a polyhedron out of
marshmallows and toothpicks.
Conclusion

The polyhedron and the prism are
important concepts in the field of
geometry. Polypro is a tactful method
in teaching these theories. Elementary
and secondary teachers can benefit
form using the visual aid of polypro to
teach geometry.