Download part2

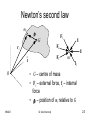
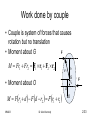
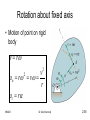
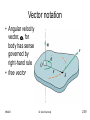
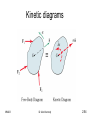
MM203
Mechanics of
Machines: Part 2
MM203
Dr. Alan Kennedy
2:1
Kinetics of systems of particles
• Extension of basic principles to general
systems of particles
– Particles with light links
– Rigid bodies
– Rigid bodies with flexible links
– Non-rigid bodies
– Masses of fluid
MM203
Dr. Alan Kennedy
2:2
Newton’s second law
mi
ri
F1
G
F2
ri
_
r
O
MM203
f1
F3
f2
mi
f3
• G – centre of mass
• Fi – external force, fi – internal
force
• ri – position of mi relative to G
Dr. Alan Kennedy
2:3
Newton’s second law
• By definition
mr

r
m
 mr   m r
i i
i
i i
• For particle i
F1  F2  F3    f1  f 2  f3    miri
• Adding equations for all particles
 F   f   m r
i i
MM203
Dr. Alan Kennedy
2:4
Newton’s second law
• Differentiating mr   miri w.r.t. time
• gives
mr   miri
• Also
• so
f  0


F

m
r
 ma

• (principle of motion of the mass centre)
MM203
Dr. Alan Kennedy
2:5
Newton’s second law
• Note that is the acceleration of the instantaneous
mass centre – which may vary over time if body not
rigid.
F
x
 max , etc.
• Note that the sum of forces is in the same direction
as the acceleration of the mass centre but does not
necessarily pass through the mass centre
MM203
Dr. Alan Kennedy
2:6
Example
• Three people (A, 60 kg, B, 90 kg,
and C, 80 kg) are in a boat which
glides through the water with
negligible resistance with a speed
of 1 knot. If the people change
position as shown in the second
figure, find the position of the boat
relative to where it would be if they
had not moved. Does the
sequence or timing of the change
in positions affect the final result?
(Answer: x = 0.0947 m). (Problem 4/15,
0.6 m
1.8 m
2.4 m
A
B
C
1 knot
x
1.2 m
1.8 m
B
1.2 m
C
A
M&K)
MM203
Dr. Alan Kennedy
2:7
Example
• The 1650 kg car has its mass centre at G. Calculate the
normal forces at A and B between the road and the front and
rear pairs of wheels under the conditions of maximum
acceleration. The mass of the wheels is small compared with
the total mass of the car. The coefficient of static friction
between the road and the rear driving wheels is 0.8. (Answer:
NA = 6.85 kN, NB = 9.34 kN). (Problem 6/5, M&K)
MM203
Dr. Alan Kennedy
2:8
Work-energy
• Work-energy relationship for mass i is
U12 i  Ti
• where (U1-2)i is the work done on mi during a
period of motion by the external and internal
forces acting on it.
• Kinetic energy of mass i is
2
2
1
1
Ti  2 mi vi  2 mi ri
MM203
Dr. Alan Kennedy
2:9
Work-energy
• For entire system
 U    T
1 2 i
i
or
U1 2  T
or
T1  U1 2  T2
MM203
Dr. Alan Kennedy
2:10
Work-energy
• Note that no net work is done by internal
forces.
• If changes in potential energy possible
(gravitational and elastic) then
T1  Vg1  Ve1  U12  T2  Vg 2  Ve 2
• as for single particle
MM203
Dr. Alan Kennedy
2:11
Work-energy
•
•
•
•
T   mi vi
For system
v i  v  ρ i
Now
2
and note that
vi  vi  vi
so
T   12 mi v  ρ i  v  ρ i 
1
2
2
  mi v   mi ρ i   mi v ρ i
1
2
MM203
2
1
2
Dr. Alan Kennedy
2
2:12
Work-energy
• Since ri is measured from G,
m ρ
i
• Now
 m v  ρ
i
i
i
0
 v   mi ρ i 
d
v   mi ρ i  0
dt
MM203
Dr. Alan Kennedy
2:13
Work-energy
• Therefore
T   mi v   mi ρ i
1
2
2
1
2
2
• i.e. energy is that of translation of mass-centre
and that of translation of particles relative to
mass-centre
MM203
Dr. Alan Kennedy
2:14
Example
y
1
x
m
45°
r
• The two small spheres, each of mass
m, are rigidly connected by a rod of
negligible mass and are released in the
position shown and slide down the
smooth circular guide in the vertical
plane. Determine their common velocity
v as they reach the horizontal dashed
position. Also find the force R between
sphere 1 and the guide the instant
before the sphere reaches position A.
(Answer: v = 1.137(gr)½, R = 2.29mg).
2
(Problem 4/9, M&K)
m
1
2
A
MM203
Dr. Alan Kennedy
2:15
Rigid body
T   mi v   mi ρ i
2
1
2
1
2
2
• Motion of particles relative to mass-centre can
only be due to rotation of body
T  mv   mi ρ i
1
2
2
1
2
2
• Velocity of particles due to rotation depends
on angular velocity and the distance to centre
of rotation. Where is centre of rotation?
• Need to examine kinematics of rotation
MM203
Dr. Alan Kennedy
2:16
Plane kinematics of rigid bodies
• Rigid body
– distances between points remains unchanged
– position vectors, as measured relative to coordinate
system fixed to body, remain constant
• Plane motion
– motion of all points is on parallel planes
– Plane of motion taken as plane containing mass centre
– Body treated as thin slab in plane of motion – all points on
body projected onto plane
MM203
Dr. Alan Kennedy
2:17
Kinematics of rigid bodies
MM203
Dr. Alan Kennedy
2:18
Translation
• All points move in parallel lines or along
congruent curves.
• Motion is completely specified by motion of
any point – therefore can be treated as particle
• Analysis as developed for particle motion
MM203
Dr. Alan Kennedy
2:19
Kinematics of rigid bodies
MM203
Dr. Alan Kennedy
2:20
Rotation about fixed axis
• All particles move in circular paths about axis of
rotation
• All lines on body (in plane of motion) rotate through
the same angle in the same time
• Similar to circular motion of a particle
T   mi ρ i   mi ri   
1
2
2
1
2
2
2
1
2
2
2
1
m
r


 i iO 2 I O
2
• where riO is distance to O, the centre of rotation, and
IO is mass moment of inertia about O
MM203
Dr. Alan Kennedy
2:21
Mass moment of inertia
• Mass moment of inertia in rotation is
equivalent to mass in translation
• Rotation and translation are analogous
T  12  2 I O
MM203
Dr. Alan Kennedy
2:22
General plane motion
• Combination of translation and rotation
• Principles of relative motion used
MM203
Dr. Alan Kennedy
2:23
Rotation
• Angular positions of two
lines on body are
measured from any
fixed reference direction
 2  1  
 2  1
2  1
2  1
MM203
Dr. Alan Kennedy
2:24
Rotation
• All lines on a rigid body in its plane of motion
have the same angular displacement, the
same angular velocity, and the same angular
acceleration
• Angular motion does not require the presence
of a fixed axis about which the body rotates
MM203
Dr. Alan Kennedy
2:25
Angular motion relations
• Angular position, angular velocity, and angular
acceleration




  ,   
• Similar to relationships between s, v, and a.
• Also, combining relationships and cancelling
out dt
 d   d
MM203
Dr. Alan Kennedy
2:26
Angular motion relations
• If constant angular acceleration
   0  t
  0  2    0 
2
2
   0   0 t  t
1
2
2
• Direction of +ve sense must be consistent
• Analogous to rectilinear motion with constant a
• Same procedures used in analysis
MM203
Dr. Alan Kennedy
2:27
Example
• The angular velocity of a gear is controlled according to  =
12 – 3t2 where , in radians per second, is positive in the
clockwise sense and where t is the time in seconds. Find the
net angular displacement  from the time t = 0 to t = 3 s.
Also find the total number of revolutions N through which the
gear turns during the 3 seconds. (Answer:  = 9 rad, N =
3.66 rev). (Problem 5/5, M&K)
MM203
Dr. Alan Kennedy
2:28
Kinetic energy of rigid body
T  mv   mi ρ i 
2
1
2
1
2
2
1
2
mv   mi riG   mv   I
2
2
1
2
2
1
2
2
T  12 mv 2  12  2 I
1
2
2
O
OG
G
• If rotation about O
2
T  mOG  2  12  2 I
1
2
MM203
Dr. Alan Kennedy
2:29
Parallel axis theorem
• Now (P.A.T.)
I O  I  mOG
2
• and so
T   IO
1
2
MM203
2
Dr. Alan Kennedy
2:30
Radius of gyration
• Radius of gyration
I
2
k
or I  k m
m
• Mass moment of inertia of point mass m at
radius of gyration is the same as that for body
• P.A.T.
MM203
kO  kG  OG
2
2
Dr. Alan Kennedy
2
2:31
Work done on rigid body
F
U   F  dr
G
G
dr
MM203
Dr. Alan Kennedy
2:32
Work done by couple
• Couple is system of forces that causes
rotation but no translation
F
• Moment about G
M  Fr1  Fr2  F1  r1  F2  r2
r1
r1
G
r2
• Moment about O
F
d
M  F r1  d   F d  r2   F r1  r2 
MM203
Dr. Alan Kennedy
O
2:33
Work done by couple
• Moment vector is a free vector
• Forces have turning effect or torque
• Torque is force by perpendicular distance
between forces
• Work done
U   Md
• positive or negative
MM203
Dr. Alan Kennedy
2:34
Forces and couples
• Torque is
F1
  F1r1  F2r2
r1
• Also unbalanced force
 F F  F
1
MM203
G
r2
F2
2
Dr. Alan Kennedy
2:35
Work-energy principle
• When applied to system of connected bodies
only consider forces/moments of system –
ignore internal forces/moments.
• If there is significant friction between
components then system must be
dismembered
MM203
Dr. Alan Kennedy
2:36
Example
• A steady 22 N force is applied
normal to the handle of the handoperated grinder. The gear inside
the housing with its shaft and
attached handle have a combined
mass of 1.8 kg and a radius of
gyration about their axis of 72
mm. The grinding wheel with its
attached shaft and pinion (inside
housing) have a combined mass
of 0.55 kg and a radius of
gyration of 54 mm. If the gear
ratio between gear and pinion is
4:1, calculate the speed of the
grinding wheel after 6 complete
revolutions of the handle starting
from rest. (Answer: N = 3320
rev/min). (Problem 6/119, M&K)
MM203
Dr. Alan Kennedy
2:37
Rotation about fixed axis
• Motion of point on rigid
body
v  r
2
v
an  r  v 
r
at  r
2
MM203
Dr. Alan Kennedy
2:38
Vector notation
• Angular velocity
vector, , for
body has sense
governed by
right-hand rule
• free vector
MM203
Dr. Alan Kennedy
2:39
Vector notation
• Velocity vector of point A
v  r  ω  r
• What are magnitude and direction of this
vector?
• Note that
r  ω  v
MM203
Dr. Alan Kennedy
2:40
Vector notation
• Acceleration of point
 r
a  v  ω  r  ω
 r
 ω  ω  r   ω
 ω v  αr
MM203
Dr. Alan Kennedy
2:41
Vector notation
• Vector equivalents
v  ωr
an  ω  ω  r 
at  α  r
• Can be applied in 3D except then angular
velocity can change direction and magnitude
MM203
Dr. Alan Kennedy
2:42
Example
• The T-shaped body rotates about
a horizontal axis through O. At
the instant
represented, its
angular velocity is  = 3 rad/s
and its angular acceleration is 
= 14 rad/s2. Determine the
velocity and acceleration of (a)
point A and (b) point B. Express
your results in terms of
components along the n- and taxes shown. (Answer: vA = 1.2et
m/s, aA = −5.6et + 3.6en m/s2, vB =
1.2et + 0.3en m/s, aB = −6.5et +
2.2en m/s2). (Problem 5/2, M&K)
MM203
Dr. Alan Kennedy
2:43
Example
• The two V-belt pulleys form an
integral unit and rotate about the
fixed axis at O. At a certain instant,
point A on the belt of the smaller
pulley has a velocity vA = 1.5 m/s,
and the point B on the belt of the
larger pulley has an acceleration
aB = 45 m/s2 as shown. For this
instant determine the magnitude of
the acceleration aC of the point C
and sketch the vector in your
solution. (Answer: aC = 149.6 m/s2).
(Problem 5/16, M&K)
MM203
Dr. Alan Kennedy
2:44
Linear impulse and momentum
• Returning to general system: Linear momentum of
mass i is
G i  mi v i
• For system (assuming m does not change with time)
G   mi v i   mi v  ρ i  
d
 mi v  dt  miρi  v mi  0
 G  mv
MM203
Dr. Alan Kennedy
2:45
Linear impulse and momentum
• Differentiating w.r.t. time
  mv  F
G

• Same as for single particle – only applies if
mass constant
• Same for rigid body
MM203
Dr. Alan Kennedy
2:46
Example
• The 300 kg and 400 kg mine cars are rolling in opposite directions along
a horizontal track with the speeds shown. Upon impact the cars become
coupled together. Just prior to impact, a 100 kg boulder leaves the
delivery chute and lands in the 300 kg car. Calculate the velocity v of the
system after the boulder has come to a rest relative to the car. Would
the final velocity be the same if the cars were coupled before the
boulder dropped? (Answer: v = 0.205 m/s). (Problem 4/11, M&K)
1.2 m/s
30°
MM203
100 kg
300 kg
400 kg
0.6 m/s
0.3 m/s
Dr. Alan Kennedy
2:47
Angular impulse and momentum
• Considered about a fixed point O and about
the mass centre.
mi
ri
G
ri
_
r
O (fixed)
MM203
Dr. Alan Kennedy
2:48
Angular impulse and momentum
• About O
H O   ri  mi v i 
   r  m v    r  m v 
H
O
i
i i
i
i i
• First term is zero since vi × vi =0 so
   r  m a    r  F 
H
O
i
i i
i
i
• - sum of all external moments (net moment of internal
forces is zero)
  M
H
O
O
MM203
Dr. Alan Kennedy
H O   M O
2:49
Angular impulse and momentum
• About O: same as for single particle. As before,
does not apply if mass is changing.
• About G
  M
H
G
G
H G   M G
MM203
Dr. Alan Kennedy
2:50
Example
• The two balls are attached to a light
rod which is suspended by a cord
from the support above it. If the balls
and rod, initially at rest, are struck
by a force F = 60 N, calculate the
corresponding acceleration aˉ of the
mass centre and the rate d2/dt2 at
which the angular velocity of the bar
is changing. (Answer: aˉ = 20 m/s2,
d2/dt2 = 336 rad/s2). (Problem 4/17, M&K)
MM203
Dr. Alan Kennedy
175 mm
75 mm
150 mm
F
2 kg
250 mm
1 kg
2:51
Rigid body
• Angular momentum
• Planar motion
HO   ri  mi vi   I Oω
H O  I O
H G  Iω
H G  I
H O  I ω  rG / O  mv 
H O  I  mv OG
MM203
Dr. Alan Kennedy
2:52
Rigid body
• Angular acceleration
  M  I α
H
O
O
O
H O  I O
   M  Iα
H
G
G
H G  I 
d

H O  I α  rG / O  mv 
dt
H O  I  ma OG
MM203
Dr. Alan Kennedy
2:53
Kinetic diagrams
MM203
Dr. Alan Kennedy
2:54
Kinetic diagrams - translation
• Alternative moment
equation for
rectilinear
translation
M
MM203
A
0,
M
P
 ma d
Dr. Alan Kennedy
2:55
Kinetic diagrams - translation
• Alternative moment
equation for
curvilinear
translation
M
MM203
A
0,
M
B
 mat d A
Dr. Alan Kennedy
2:56
Example
• The cart B moves to the right with
acceleration a = 2g. If the steady-state
angular deflection of the uniform
slender rod of mass 3 m is observed to
be 20°, determine the value of the
torsional spring constant K. The
spring, which exerts a moment M = K
on the rod, is undeformed when the
rod is vertical. The values of m and l
are 0.5 kg and 0.6 m, respectively.
Treat the small end sphere of mass m
as a particle. (Answer: K = 46.8
N·m/rad). (Problem 6/16, M&K)
MM203
Dr. Alan Kennedy
2:57
Example
• The mass of gear A is 20 kg
and its centroidal radius of
gyration is 150 mm. The
mass of gear B is 10 kg and
its centroidal radius of
gyration
is
100
mm.
Calculate
the
angular
acceleration of gear B when
a torque of 12 N·m is applied
to the shaft of gear A.
Neglect friction. (Answer: B
= 25.5 rad/s2 (CCW)). (Problem
6/46, M&K)
MM203
Dr. Alan Kennedy
2:58
Example
• The 28 g bullet has a
horizontal velocity of 500 m/s
when it strikes the 25 kg
compound pendulum, which
has a radius of gyration of kO
= 925 mm. If the distance h =
1075 mm, calculate the
angular velocity  of the
pendulum with its embedded
bullet immediately after the
impact. (Answer:  = 0.684
rad/s) (Problem 6/174, M&K)
MM203
Dr. Alan Kennedy
2:59
Plane kinematics: absolute motion
• Absolute motion analysis
– Get geometric relationships
– Get time derivatives to determine velocity and
acceleration
– Straightforward if geometry is straightforward
– Must be consistent with signs
MM203
Dr. Alan Kennedy
2:60
Example
• Point A is given a constant acceleration a to the right starting from rest
with x essentially 0. Determine the angular velocity  of link AB in terms
of x and a. (Problem 5/24, M&K)
• Answer:

MM203
2ax
4b 2  x 2
Dr. Alan Kennedy
2:61
Example
• The wheel of radius r rolls without slipping, and its centre O has a
constant velocity vO to the right. Determine expressions for the velocity v
and acceleration of point A on the rim by differentiating its x- and ycoordinates. Represent your result graphically as vectors on your sketch
and show that v is the vector sum of two vO vectors. (Problem 5/25, M&K)
• Answer:
v  vO 21  sin   ,
2
vO
a
towards O
r
MM203
Dr. Alan Kennedy
2:62
Example
• One of the most common mechanisms is the slider-crank. Express the
angular velocity AB and the angular acceleration AB of the connecting
rod AB in terms of the crank angle  for a given constant crank speed 0.
Take AB and AB to be positive counter-clockwise. (Problem 5/54, M&K)
• Answer:
 AB
 AB
MM203
r 0

l
cos 
r2
1  2 sin 2 
l
r2
1
2
2
r 0
l

sin 
3
2
2
l
 r

1  2 sin 2  
 l

Dr. Alan Kennedy
2:63
Plane kinematics: relative velocity
• Two points on same rigid body.
• Motion of one relative to the other must be circular
since distance between them is constant.
MM203
Dr. Alan Kennedy
2:64
Plane kinematics: relative velocity
• Relative linear velocity is always in direction
perpendicular to line joining points
v A  v B  v A/ B
v A / B  ω  rA / B
v A / B  AB
MM203
Dr. Alan Kennedy
2:65
Plane kinematics: relative velocity
MM203
Dr. Alan Kennedy
2:66
Plane kinematics: relative velocity
• Relative velocity principles may also be used
in cases where there is constrained sliding
contact between two links – A and B may be
on different links
MM203
Dr. Alan Kennedy
2:67
Example
• Determine
the
angular
velocity of the telescoping
link AB for the position shown
where the driving links have
the
angular
velocities
indicated. (Answer: AB = 0.96
rad/s). (Problem 5/61, M&K)
MM203
Dr. Alan Kennedy
2:68
Example
• For an interval of its motion
the piston rod of the hydraulic
cylinder has a velocity VA =
1.2 m/s as shown. At a
certain instant  =  = 60°.
For this instant determine the
angular velocity BC of the
link BC. (Answer: BC = 15.56
rad/s). (Problem 5/66, M&K)
MM203
Dr. Alan Kennedy
2:69
Example
• The mechanism is designed to
convert from one rotation to
another. Rotation of link BC is
controlled by the rotation of the
curved slotted arm OA which
engages pin P. For the instant
represented  = 30° and , the
angle between the tangent to the
curve at P and the horizontal, is
40°. If the angular velocity of OA is
as shown, determine the velocity of
the point C. (Answer: vC = 4.33
m/s). (Problem 5/85, M&K)
MM203
Dr. Alan Kennedy
2:70
Relative acceleration
a A  a B  a A / B  a B  a A / B n  a A / B t
2
vA/ B
2
a A / B n 
 AB
AB
a A / B t  vA / B  AB
• May need to know velocities first
MM203
Dr. Alan Kennedy
2:71
Example
• If OA has a CCW angular
velocity 0 = 10 rad/s (giving
BC = 5.83 rad/s and AB =
2.5 rad/s), calculate the
angular acceleration of link
AB for the position where
the coordinates of A are x =
−60 mm and y = 80 mm. Link
BC is vertical for this
position. (Answer: AB = 2.5
rad/s2). (Problem 5/137, M&K)
MM203
Dr. Alan Kennedy
2:72