* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 21
Wave interference wikipedia , lookup
Crystal radio wikipedia , lookup
Superconductivity wikipedia , lookup
Operational amplifier wikipedia , lookup
Galvanometer wikipedia , lookup
Spark-gap transmitter wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Power electronics wikipedia , lookup
Power MOSFET wikipedia , lookup
Electrical ballast wikipedia , lookup
Index of electronics articles wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
Current source wikipedia , lookup
Surge protector wikipedia , lookup
Switched-mode power supply wikipedia , lookup
RLC circuit wikipedia , lookup
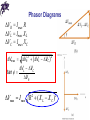
Chapter 21 Alternating Current Circuits and Electromagnetic Waves AC Circuit • An AC circuit consists of a combination of circuit elements and an AC generator or source • The output of an AC generator is sinusoidal and varies with time according to the following equation Δv = ΔVmax sin 2ƒt • Δv: instantaneous voltage • ΔVmax is the maximum voltage of the generator • ƒ is the frequency at which the voltage changes, in Hz Resistor in an AC Circuit • Consider a circuit consisting of an AC source and a resistor • The graph shows the current through and the voltage across the resistor • The current and the voltage reach their maximum values at the same time • The current and the voltage are said to be in phase • The direction of the current has no effect on the behavior of the resistor Resistor in an AC Circuit • The rate at which electrical energy is dissipated in the circuit is given by i 2R • i: instantaneous current • The heating effect produced by an AC current with a maximum value of Imax is not the same as that of a DC current of the same value • The maximum current occurs for a small amount of time rms Current and Voltage • The rms current is the direct current that would dissipate the same amount of energy in a resistor as is actually dissipated by the AC current I rms Imax 2 0.707 Imax • Alternating voltages can also be discussed in terms of rms values V Vrms max 2 0.707 Vmax • The average power dissipated in resistor in an AC circuit carrying a current I is av I 2 rms R Ohm’s Law in an AC Circuit • rms values will be used when discussing AC currents and voltages • AC ammeters and voltmeters are designed to read rms values • Many of the equations will be in the same form as in DC circuits • Ohm’s Law for a resistor, R, in an AC circuit ΔVR,rms = Irms R • The same formula applies to the maximum values of v and i Chapter 21 Problem 4 The figure shows three lamps connected to a 120-V AC (rms) household supply voltage. Lamps 1 and 2 have 150W bulbs; lamp 3 has a 100-W bulb. Find the rms current and the resistance of each bulb. Capacitors in an AC Circuit • Consider a circuit containing a capacitor and an AC source • The current starts out at a large value and charges the plates of the capacitor • There is initially no resistance to hinder the flow of the current while the plates are not charged • As the charge on the plates increases, the voltage across the plates increases and the current flowing in the circuit decreases Capacitors in an AC Circuit • The current reverses direction • The voltage across the plates decreases as the plates lose the charge they had accumulated • The voltage across the capacitor lags behind the current by 90° • The impeding effect of a capacitor on the current in an AC circuit is called the capacitive reactance (ƒ is in Hz, C is in F, XC is in ohms): 1 XC • Ohm’s Law for a capacitor in an AC circuit ΔVC,rms = Irms XC 2 ƒC Inductors in an AC Circuit • Consider an AC circuit with a source and an inductor • The current in the circuit is impeded by the back emf of the inductor • The voltage across the inductor always leads the current by 90° • The effective resistance of a coil in an AC circuit is called its inductive reactance (ƒ is in Hz, L is in H, XL is in ohms): XL = 2ƒL • Ohm’s Law for the inductor: ΔVL,rms = Irms XL The RLC Series Circuit • The resistor, inductor, and capacitor can be combined in a circuit • The current in the circuit is the same at any time and varies sinusoidally with time The RLC Series Circuit • The instantaneous voltage across the resistor is in phase with the current • The instantaneous voltage across the inductor leads the current by 90° • The instantaneous voltage across the capacitor lags the current by 90° Phasor Diagrams • To account for the different phases of the voltage drops, vector techniques are used • Represent the voltage across each element as a rotating vector, called a phasor • The diagram is called a phasor diagram • The voltage across the resistor is on the +x axis since it is in phase with the current Phasor Diagrams • The voltage across the inductor is on the +y since it leads the current by 90° • The voltage across the capacitor is on the –y axis since it lags behind the current by 90° • The phasors are added as vectors to account for the phase differences in the voltages • ΔVL and ΔVC are on the same line and so the net y component is ΔVL - ΔVC Phasor Diagrams • The voltages are not in phase, so they cannot simply be added to get the voltage across the combination of the elements or the voltage source Vmax VR2 (VL VC )2 VL VC tan VR • is the phase angle between the current and the maximum voltage • The equations also apply to rms values Phasor Diagrams ΔVR = Imax R ΔVL = Imax XL ΔVC = Imax XC Vmax VR2 (VL VC )2 VL VC tan VR Vmax I max R ( X L X C ) 2 2 Impedance of a Circuit • The impedance, Z, can also be represented in a phasor diagram Z R2 ( X L X C )2 X L XC tan R • Ohm’s Law can be applied to the impedance ΔVmax = Imax Z • This can be regarded as a generalized form of Ohm’s Law applied to a series AC circuit Summary of Circuit Elements, Impedance and Phase Angles Problem Solving for AC Circuits • Calculate as many unknown quantities as possible (e.g., find XL and XC) • Be careful with units – use F, H, Ω • Apply Ohm’s Law to the portion of the circuit that is of interest • Determine all the unknowns asked for in the problem Chapter 21 Problem 26 A 60.0-V resistor is connected in series with a 30.0-µF capacitor and a generator having a maximum voltage of 1.20 × 102 V and operating at 60.0 Hz. Find the (a) capacitive reactance of the circuit, (b) impedance of the circuit, and (c) maximum current in the circuit. (d) Does the voltage lead or lag the current? Power in an AC Circuit • No power losses are associated with pure capacitors and pure inductors in an AC circuit • In a capacitor, during 1/2 of a cycle energy is stored and during the other half the energy is returned to the circuit • In an inductor, the source does work against the back emf of the inductor and energy is stored in the inductor, but when the current begins to decrease in the circuit, the energy is returned to the circuit Power in an AC Circuit • The average power delivered by the generator is converted to internal energy in the resistor Pav = Irms ΔVR,rms ΔVR, rms = ΔVrms cos Pav = Irms ΔVrms cos • cos is called the power factor of the circuit • Phase shifts can be used to maximize power outputs Chapter 21 Problem 35 An inductor and a resistor are connected in series. When connected to a 60-Hz, 90-V (rms) source, the voltage drop across the resistor is found to be 50 V (rms) and the power delivered to the circuit is 14 W. Find (a) the value of the resistance and (b) the value of the inductance. Resonance in an AC Circuit • Resonance occurs at the frequency, ƒ0, where the current has its maximum value I rms Vrms R (X L XC ) 2 2 • To achieve maximum current, the impedance must have a minimum value • This occurs when XL = XC and 1 2f 0 L 2f 0C f0 1 2 LC Resonance in an AC Circuit • Theoretically, if R = 0 the current would be infinite at resonance • Real circuits always have some resistance • Tuning a radio: a varying capacitor changes the resonance frequency of the tuning circuit in your radio to match the station to be received Transformers • An AC transformer consists of two coils of wire wound around a core of soft iron • The side connected to the input AC voltage source is called the primary and has N1 turns • The other side, called the secondary, is connected to a resistor and has N2 turns • The core is used to increase the magnetic flux and to provide a medium for the flux to pass from one coil to the other B Transformers B V1 N1 V2 N 2 t t • The rate of change of the flux is the same for both coils, so the voltages are related by N2 V2 N1 V1 • When N2 > N1, the transformer is referred to as a step up transformer and when N2 < N1, the transformer is referred to as a step down transformer • The power input into the primary equals the power output at the secondary I1V1 I 2 V2 Chapter 21 Problem 45 An AC power generator produces 50 A (rms) at 3 600 V. The voltage is stepped up to 100 000 V by an ideal transformer, and the energy is transmitted through a long-distance power line that has a resistance of 100 Ω. What percentage of the power delivered by the generator is dissipated as heat in the power line? LC Circuit • When the switch is closed, oscillations occur in the current and in the charge on the capacitor • When the capacitor is fully charged, the total energy of the circuit is stored in the electric field of the capacitor • At this time, the current is zero and no energy is stored in the inductor • As the capacitor discharges, the energy stored in the electric field decreases • At the same time, the current increases and the energy stored in the magnetic field increases LC Circuit • When the capacitor is fully discharged, there is no energy stored in its electric field • The current is at a maximum and all the energy is stored in the magnetic field in the inductor • The process repeats in the opposite direction • There is a continuous transfer of energy between the inductor and the capacitor Maxwell’s Theory • Electricity and magnetism were originally thought to be unrelated • Maxwell’s theory showed a close relationship between all electric and magnetic phenomena and proved that electric and magnetic fields play symmetric roles in nature • Maxwell hypothesized that a changing electric field would produce a magnetic field • He calculated the speed of light – 3x108 m/s – and concluded that light and other electromagnetic waves consist of James Clerk Maxwell fluctuating electric and magnetic fields 1831-1879 Maxwell’s Theory • Stationary charges produce only electric fields • Charges in uniform motion (constant velocity) produce electric and magnetic fields • Charges that are accelerated produce electric and magnetic fields and electromagnetic waves • A changing magnetic field produces an electric field • A changing electric field produces a magnetic field • These fields are in phase and, at any point, they both reach their maximum value at the James Clerk Maxwell same time 1831-1879 Hertz’s Experiment • Hertz was the first to generate and detect electromagnetic waves in a laboratory setting • An induction coil was connected to two large spheres forming a capacitor • Oscillations were initiated by short voltage pulses • The inductor and capacitor formed the transmitter Heinrich Rudolf Hertz 1857 – 1894 Hertz’s Experiment • Several meters away from the transmitter was the receiver • This consisted of a single loop of wire connected to two spheres • It had its own inductance and capacitance • When the resonance frequencies of the transmitter and receiver matched, energy transfer occurred between them Heinrich Rudolf Hertz 1857 – 1894 Hertz’s Results • Hertz hypothesized the energy transfer was in the form of waves (now known to be electromagnetic waves) • Hertz confirmed Maxwell’s theory by showing the waves existed and had all the properties of light waves (with different frequencies and wavelengths) • Hertz measured the speed of the waves from the transmitter (used the waves to form an interference pattern and calculated the wavelength) • The measured speed was very close to 3 x 108 m/s, the known speed of light, which provided evidence in support of Maxwell’s theory Electromagnetic Waves Produced by an Antenna • When a charged particle undergoes an acceleration, it must radiate energy in the form of electromagnetic waves • Electromagnetic waves are radiated by any circuit carrying alternating current • An alternating voltage applied to the wires of an antenna forces the electric charge in the antenna to oscillate Electromagnetic Waves Produced by an Antenna • Two rods are connected to an ac source, charges oscillate between the rods (a) • As oscillations continue, the rods become less charged, the field near the charges decreases and the field produced at t = 0 moves away from the rod (b) • The charges and field reverse (c) and the oscillations continue (d) Electromagnetic Waves Produced by an Antenna • Because the oscillating charges in the rod produce a current, there is also a magnetic field generated • As the current changes, the magnetic field spreads out from the antenna • The magnetic field is perpendicular to the electric field Properties of Electromagnetic Waves • Electromagnetic waves are transverse • The E and B fields are perpendicular to each other and both fields are perpendicular to the direction of motion • Electromagnetic waves travel at the speed of light (light is an electromagnetic wave): c 1 o o E c B • The ratio of the electric field to the magnetic field is equal to the speed of light Properties of Electromagnetic Waves • Electromagnetic waves carry energy as they travel through space, and this energy can be transferred to objects placed in their path • Energy carried by em waves is shared equally by the electric and magnetic fields Average power per unit area 2 2 Emax Bmax Emax c Bmax I 2o 2oc 2o • Electromagnetic waves transport linear momentum as well as energy The Spectrum of EM Waves • Types of electromagnetic waves are distinguished by their frequencies (wavelengths): c = ƒ λ • There is no sharp division between one kind of em wave and the next – note the overlap between types of waves The Spectrum of EM Waves • Radio waves are used in radio and television communication systems • Microwaves (1 mm to 30 cm) are well suited for radar systems + microwave ovens are an application • Infrared waves are produced by hot objects and molecules and are readily absorbed by most materials The Spectrum of EM Waves • Visible light (a small range of the spectrum from 400 nm to 700 nm) – part of the spectrum detected by the human eye • Ultraviolet light (400 nm to 0.6 nm): Sun is an important source of uv light, however most uv light from the sun is absorbed in the stratosphere by ozone The Spectrum of EM Waves • X-rays – most common source is acceleration of high-energy electrons striking a metal target, also used as a diagnostic tool in medicine • Gamma rays: emitted by radioactive nuclei, are highly penetrating and cause serious damage when absorbed by living tissue Answers to Even Numbered Problems Chapter 21: Problem 8 (a) 141 mA (b) 235 mA Answers to Even Numbered Problems Chapter 21: Problem 14 (a) 12.6 Ω (b) 6.19 A (c) 8.75 A Answers to Even Numbered Problems Chapter 21: Problem 40 (a) Z = R = 15 Ω (b) 41 Hz (c) At resonance (d) 2.5 A Answers to Even Numbered Problems Chapter 21: Problem 64 (a) 6.0036 × 1014 Hz (b)increases by 3.6 × 1011 Hz