Download Quantum Computation

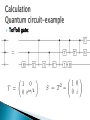
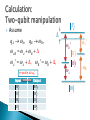
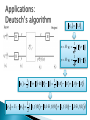
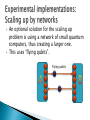
Jonathan Coslovsky
March 2008








Introduction
The qubit
Calculation (gates)
Decoherence and error correction
Applications
Experimental implementations
Experimental progress timescale
Summery

Silicon microprocessor chip – Since 1960s.
The IBM System 360/20
1966

Moore’s law – The number of transistors placed on an
integrated circuit is increasing exponentially.
Polynomial computing tasks – P.
 Non-Polynomial computing tasks-NP.
 Example: Factorization:
15
3x5
91
7x13
703
?x?
19x37
8876044532898802067
???????x???????
Answer: 5915587277 x 1500450271
Why is this important? The principle of RSA.


Solution #1: wait for a few years for a better
(classical) computer.
◦ Problem:
Today: L< 1μm. (L-Transistor size)
Quantum effects become important: L~λ~nm.
(λ-de Broglie wavelength of electrons).
Individual atom size: L~a0~Ǻ.
Moore’s law will eventually break down.

Solution #2: Find a new computing technique.

The idea: Take advantage of QM phenomena,
such as superposition and entanglement.
Is it possible?
1994-Shor, P algorithm for factoring numbers.


Classical bit: 0 or 1.
voltage on a transistor, magnetization of a
ferromagnetic material, or intensity of a pulse
of light.

Qubit: Superposition in a two state system

01 0
Where
E
|1>
  c0 0  c1 1 .
|0>

3 qubits register:
  c000 000  c001 001  c010 010  c011 011 
 c100 100  c101 101  c110 110  c111 111


Vector representation:
 c000 


c
   001 




c
 111 

i , j , k  0,1
An N-qubit register is described by 2N
(complex) amplitudes.
2
cijk  1
Quantum system Physical property
0
1
Photon
Linear
polarization
Horizontal
Vertical
Photon
Circular
polarization
Left
Right
Nucleus
Spin
Up
Down
Electron
Spin
Up
Down
Tow-level atom
Excitation state
Ground state
Excited state
Josephson
junction
Electric charge
N Cooper pairs
N+1 Cooper
pairs
Superconducting
loop
Magnetic flux
Up
Down

A single qubit can be represented on a Bloch
sphere:


  cos( ) 0  e sin( ) 1
2
i
2
1
0
Single bit-NOT gate
Input bit
Output bit
0
1
1
0
Two bits-C-NOT gate
Control
Input
Target
Input
Target
Output
0
0
0
0
1
1
1
0
1
1
1
0
But what is the meaning in a qubit?
Quantum gate
Matrix representation
Bloch sphere
representation
NOT(X)
0 1


1
0


Rotation of π about
the x-axis
Z
1 0 


0

1


Rotation of π about
the z-axis
1 1 1 


1

1
2

Rotation of π about
the z-axis, rotation of
π/2 about the y-axis
Hadamard (H)


The controlled-NOT gate:
i.e.
U CNOT
1

0

 
0

0
0 0
1 0
0 0
0 1
1

0

U CNOT 
0

0
0   c00   c00 
   
0   c01   c01 

1   c10   c11 
   
0  c11   c10 
0
1
0
0
0
0
0
1
0

0
1

0
Example:
ControlInput  Target Input  0
Step 1:
Step 2:
 1  1 1 1  1  1 1
H 

  
 
0
1

1
0
2
2  1
 
 
1
1
 
 0  1   0   00  10
2
2
1

0
 ' 
0

0
0
1
0
0
0
0
0
1

0
1
1

 
 
0 1 0 1 0 1


00  11

1 2 1
2 0
2

 
 
0
0
1



Any qubit gate can be formed by combining
C-NOT gates with single-qubit operations.
Example:
1 0 0 0
U SWAP


0
0
1
0


0 1 0 0


0
0
0
1



Toffoli gate:


Every unitary transformation U can be
represented as a rotation over the Bloch
Sphere.
Every single-qubit operator U can be
decomposed to:
U  e Rz (3 ) Ry ( 2 ) Rz (1 )
i

For Example:
Rx ( )  Rz ( / 2) Ry ( ) Rz ( / 2)
 X  Rz ( / 2) Ry ( ) Rz ( / 2)

Lets consider a 2-level atom:
◦ Rotation is achieved by a pulse.
◦  is set by the optical phase of the
pulse.

◦ Pulse area:
01

01  Dipole moment
 0 (t )  Electric field


0
(t )dt

11
Assume
q A   A , qB   B ,

 AB   A  B  
 A '   A  ,  B '   B  ,
π-pulse at ωB’
Input
Output
00
01
10
00
01
11
11
10
A '
B '
01
A
10
00
B


Control qubit – Excitation level of a cooled
9Be+ ion in a harmonic trap.
Target qubit – 2 hyperfine levels of the ion.




Interactions with environment
decoherence
loss of information.
In order to increase decoherence time,
typically low temperatures are used.
Quantum systems are fragile.
We need
quantum error correction algorithms.
Error rates are proportional to the ratio of
operating time to decoherence time.


Dephasing time: T2.
Number of operations:
T2
Nop 
Top
System
T2(s)
Top(s)
Nop
Nuclear spin
104
10-3
107
Ion trap
100
10-6 (e)
106
Excitation (quantum dot)
10-9 (e)
10-12 (e)
103
Electron spin (quantum dot)
10-7
10-12
105
Superconducting flux qubit
10-8 (e)
10-10 (e)
102 (e)



The idea: determine if a single bit function
f(x) is constant or balanced.
Classical computer-2 calls.
Quantum computer-1 call.
F(0)
F(1)
F1
0
0
constant
F2
1
0
Balanced
F3
0
1
Balanced
f4
1
1
constant
 0  0,1
1
0 1
2
1
y  H  q2 
0 1
2
x  H  q1 
1 
 2  U f  1 
1
1
0

1

0

1

0, 0  0,1  1, 0  1,1





2
2

1
0, f (0)  0,1  f (0)  1, f (1)  1,1  f (1)

2

2
1
  0, f (0)  0,1  f (0)  1, f (1)  1,1  f (1)
2

If f is constant: f(0)=f(1)
2
constant
x
1
  0, f (0)  0,1  f (0)  1, f (0)  1,1  f (0)
2
1
=  0  1    f (0)  1  f (0) 
2
constant
1
 H   0  1   0

2

2
1
  0, f (0)  0,1  f (0)  1, f (1)  1,1  f (1)
2

If f is balanced: f(1)=1⊕f(0)
2
balanced
x
1
  0, f (0)  0,1  f (0)  1,1  f (0)  1, f (0)
2
1
=  0  1    f (0)  1  f (0) 
2
balanced
1
 H   0  1   1

2



Quantum search algorithm.
For example: The London telephone directory:
 Holmes, Sherlock 221b Baker Street 123 456



It is easy to find Holmes’ telephone number,
but, difficult to find the telephone 123 456.
Classical computer ~ NData/2 op.
Quantum computer ~ Sqrt(NData).
 0  0 1  0 2  ...  0
1 
 0
1
1
1
0

1

0

1

...

0



1
1
2
2
2
2
2
 1 


2


1 
N
N 2N
x
x 0

1
N Data
N Data 1

x
x 0
1
1,1,1...,1   2   0, 0,1, 0,..., 0 
N Data
N
1
N


Grover operator:
1.
2.
3.
4.
Oracle.
Hadamard gate.
CPS-conditional phase shift.
Hadamard.
◦ Oracle: a gate that checks if we have the desired
solution:
f ( x)
O x   1
x
1 x is the solution,
f ( x)  
otherwise
0

The three other steps (H, CPS,H) perform an
‘inversion about the mean’.

Example: Ndata=4, N=2 qubits.

Applying oracle:
 0  00
 1
2
 
1
1  1
 1 
1  
  0 1  1 1    0 2  1 2   2  00  01  10  11   2 1
 2
 
 1
 Suppose: target=10.
1
 
2
 
1 1 

2  1 
 
1

Inversion about the mean:
 3   0,0,1,0
Mean
This Algorithm can be used as a password cracker!





Fourier transform operation:
Classical computer (FFT) ~ n2n op. for N=2n
numbers.
Quantum Computer ~ n2 op.
But the result of QFT is stored as amplitudes, it
can not be read.
But QC can find periodicity.
1994-Peter Shor – can be used to factorize large
numbers.
Is RSA encryption in danger?




Largest prime number today (March 2008):
232582657-1.
In order to factorize a 1000 bit number,
between 1012 and 1018 qubits are required.
Until today, systems of only a few qubits have
been demonstrated.
RSA is probably safe for the next few
decades.





C.C. -> Memory required is exponential in
system size.
N two-level system -> 2N amplitudes.
A relatively small molecule of 53 atoms
requires 253~9x1015 bits~1 Petabyte=106
Gigabytes.
Q.C. -> N qubits required.
Unfortunately, on making the measurements,
we would only obtain N bits of information.
P ( L)  e
n( L )  e
 L / L0
 L / L0
Pi ( L, N )  e
 L / NL0
L
ni ( L, N )  e  L / NL0  n( L, N )  Ne  L / NL0
Nmin ( L)  L / L0  n( L, Nmin )   L / L0  e1
D. DiVincenzo: requirements for the system:
1. Scalable physically to increase the number
of qubits .
2. Possible to prepare an initial state.
3. Decoherence time >> operation time.
4. Single- and two-qubit quantum gates must
be demonstrated.
5. Possible to measure the state of each
individual qubit.



An optional solution for the scaling up
problem is using a network of small quantum
computers, thus creating a larger one.
This uses “flying qubits”.
Flying qubits






1995: Quantum C-NOT gate.
1998: 2 and 3 qubit NMR QC. Execution of
Grover’s algorithm.
2000: 5 and 7 qubit NMR QC. Execution of
order finding.
2001: Execution of Shor’s algorithm (15 was
factored).
2005: Qubyte.
2006: 12 qubit QC.
Is Moore’s law
valid on a QC?
# of qubits
QC of 1000
qubits expected
on 2032.
QC of 1
GigaQubyte only
on 2127
# of qubits (logarithmic sacle)
y = 4E-145e0.167x
10
1
1996
1998
2000
2002
Year
2004
2006
2008




Quantum computation is in some cases more
efficient than classical computation.
QC is possible, at least in principle.
Small QC systems have already been
demonstrated.
The main goal now is to scale up the systems.