Download Part I

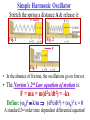
Elastic Properties of Solids
Topics Discussed in Kittel, Ch. 3, pages 73-85
Hooke's “Law”
• A property of an ideal spring of spring constant k is that
it takes twice as much force to stretch the spring twice as
far. That is, if it is stretched a distance x, the restoring
force is given by F = - kx. The spring is then said to obey
Hooke's “Law”.
• An elastic medium is one in which a disturbance can be
analyzed in terms of Hooke’s “Law” forces.
Consider the propagation of a mechanical wave
(disturbance) in a solid.
• We are interested in the case of very long wavelengths, when the
wavelength is much, much larger than the interatomic spacing:
 >> a
so that the solid can be treated as a continuous elastic
medium & the fact that there are atoms on a lattice is
irrelevant to the wave propagation.
A Prototype Hooke’s Law System
A Mass-Spring System
in which a mass m is
attached to an ideal
spring of spring
constant k. That is, the
Simple Harmonic
Oscillator
(SHO)
Simple Harmonic Oscillator
Stretch the spring a distance A & release it:
Fig. 1
Fig. 2
Fig. 3
• In the absence of friction, the oscillations go on forever.
• The Newton’s 2nd Law equation of motion is:
F = ma = m(d2x/dt2) = -kx
Define: (ω0)2  k/m  (d2x/dt2) + (ω0)2 x = 0
A standard 2nd order time dependent differential equation!
Simple Harmonic Oscillator
Hooke’s “Law” for a vertical spring (take + x as down):
Static Equilibrium:
∑Fx = 0 = mg - kx0
or x0 = (mg/k)
Newton’s 2nd Law
Equation of Motion:
This is the same as
before, but the
equilibrium position is
x0 instead of x = 0
• An Elastic Medium is defined to be one in
which a disturbance from equilibrium
obeys Hooke’s “Law” so that a local
deformation is proportional to an applied force.
• If the applied force gets too large, Hooke’s “Law”
no longer holds. If that happens the medium is no
longer elastic. This is called the Elastic Limit.
• The Elastic Limit is the point at which
permanent deformation occurs, that is, if
the force is taken off the medium, it will not
return to its original size and shape.
Sound Waves
• Sound waves are mechanical waves
which propagate through a material
medium (solid, liquid, or gas) at a speed
which depends on the elastic & inertial
properties of the medium. There are 2
types of wave motion for sound waves:
Longitudinal
and
Transverse
Sound Waves
• Because we are considering only long wavelength
mechanical waves ( >> a) the presence of atoms is
irrelevant & the medium may be treated as continuous.
Longitudinal Waves
Sound Waves
• Because we are considering only long wavelength
mechanical waves ( >> a) the presence of atoms is
irrelevant & the medium may be treated as continuous.
Longitudinal Waves
Transverse Waves
• Sound waves propagate through solids. This tells us
that wavelike lattice vibrations of wavelength long
compared to the interatomic spacing are possible.
The detailed atomic structure is unimportant for
these waves & their propagation is governed by
the macroscopic elastic properties of the crystal.
• So, the reason for discussing sound waves is that
they correspond to the low frequency, long
wavelength limit of the more general lattice
vibrations we have been considering up to now.
• At a given frequency and in a given direction in a
crystal it is possible to transmit 3 different kinds
of sound waves, differing in their direction of
polarization and in general also in their velocity.
Elastic Waves
• So, consider sound waves propagating in a solid,
when their wavelength is very long, so that the
solid may be treated as a continous medium.
Such waves are referred to as elastic waves.
Consider Longitudinal Elastic Wave
Propagation in a Solid Bar
• At the point x the
elastic displacement (or
change in length) is U(x)
& the strain e is
defined as the change
in length per unit length.
A
x x+dx
dU
e
dx
• In general, a Stress S at
a point in space is
defined as the force per
unit area at that point.
A
x x+dx
dU
e
dx
• Hooke’s “Law” tells us that, at point x &
time t in the bar, the stress S produced by an
elastic wave propagation is proportional to
the strain e. That is:
C  Young’s Modulus
• To analyze the dynamics
of the bar, choose an
arbitrary segment of
length dx as shown
above. Use Newton’s
2nd Law to write for the
motion of this segment,
A
x
x+dx
dU
e
dx
C  Young’s Modulus
 2u
(  Adx) 2   S ( x  dx)  S ( x)  A
t
Mass  Acceleration = Net Force resulting from stress
Equation of Motion
 2u
(  Adx) 2   S ( x  dx)  S ( x)  A
t
S  C.e
S
S
(
x

dx
)

S
(
x
)

dx


x
So, this becomes:
du
e
dx
 2u
 2u
(  Adx) 2  C 2 Adx
t
x
u
S  C.
x
S
 2u
 C. 2
x
x
Cancelling common terms in Adx gives:
 2u
 2u
 2 C 2
t
x
Plane wave solution:
This is the wave equation a plane
wave solution which gives the
sound velocity vs:   v k
u  Ae
i ( kx t )
s
vs 
C/
k = wave number = (2π/λ), ω = frequency, A = amplitude
• Unlike the case for the discrete lattice, the dispersion relation
ω(k) in this long wavelength limit is the simple equation:
  vs k
• At small λ (k → ∞), scattering from
discrete atoms occurs.
• At long λ (k → 0), (continuum) no
scattering occurs.
• When k increases the sound
velocity decreases.
• As k increases further, the
scattering becomes greater since the
strength of scattering increases as
the wavelength decreases, and the
velocity decreases even further.
ω
Continuum
Discrete
0
k
Speed of Sound
• The speed VL with which a longitudinal elastic wave
moves through a medium of density ρ is given by:
VL   
C

C  Bulk Modulus
ρ  Mass Density
• The velocity of sound is in general a function of the
direction of propagation in crystalline materials.
• Solids will sustain the propagation of transverse waves,
which travel more slowly than longitudinal waves.
• The larger the elastic modulus & the smaller the
density, the larger the sound speed is.
Speed of Sound for Several Common Solids
Structure
Type
Nearest
Neighbor
Distance
(A°)
Density
ρ
(kg/m3)
Elastic bulk
modulus
Y
(1010 N/m2)
Calculate
d Wave
Speed
(m/s)
Observed
speed of
sound
(m/s)
Sodium
B.C.C
3.71
970
0.52
2320
2250
Copper
F.C.C
2.55
8966
13.4
3880
3830
Aluminum
F.C.C
2.86
2700
7.35
5200
5110
Lead
F.C.C
3.49
11340
4.34
1960
1320
Silicon
Diamond
2.35
2330
10.1
6600
9150
Germanium
Diamond
2.44
5360
7.9
3830
5400
NaCl
Rocksalt
2.82
2170
2.5
3400
4730
Solid
Most calculated VL values are in reasonable agreement
with measurements. Sound speeds are of the order of 5000
m/s in typical metallic, covalent & ionic solids :