Download MATH 1113 Review Sheet for the Final Exam

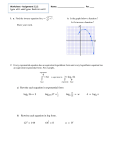
MATH 1113 Review Sheet for the Final Exam
Section 2.1 Functions
 Defining a function in words (we discussed three ways to do this)
 Different ways to specify a function: Geometrically, Analytically, Numerically, Verbally
 Relation, Domain, Codomain, Range, Dependent Variable, Independent Variable
 Function Notation , i.e. f(a) = b
 Given that f is a function, what does f(a) represent? If a is in the domain of the function f, f(a) is the value that function f
assigns to the element a. If a is not in the domain of f, f(a) is not defined.
 Operations on Functions (sum, product, difference, and quotient of functions)
 The implicit domain for a function from real numbers to real numbers is the largest subset of the real numbers for which the
formula has meaning.
Section 2.2 The Graph of a Function
 Defining the graph of a function
 Determining when a graph represents a function; the vertical line test
 Given the graph of function f, solving f(x) = k for x given k and f(x) =k for k given x using the graph.
 Reading the domain and range of a function from the graph
Section 2.3 Properties of a Function
 Even and Odd functions
 Local Extremum (local maximum, local minimum) Note the plural forms: extrema, maxima, minima
 Secant Line
 Average Rate of Change of a function over an interval, connection to the slope of a secant line
 Increasing/Decreasing/Constant on an interval
 Intercepts (horizontal intercepts, vertical intercepts)
o A function may have any nonnegative integer number of horizontal intercepts
 (i.e. have 0, 1, 2, 3, …..horizontal intercepts)
o A function has at most one vertical intercept
Section 2.4 Library of Functions
 The library of functions include the following: Linear, Constant, Identity, Square, Cube, Square Root, Cube Root,
Reciprocal, Absolute Value, and Greatest Integer functions
 For each function in the library, be familiar with the following: its graph, intervals on which the function is
increasing/decreasing/constant, its horizontal and vertical intercepts, whether it is even or odd or both or neither, its domain
and range, its local maxima and local minima (i.e. local extrema)
 piecewise-defined functions
Section 2.5 Graphing Techniques: Transformations
 Scaling (Shrinking and Stretching)
 Reflection in the horizontal axis
 Translations (Horizontal Shifts and Vertical Shifts)
 Rigid vs. Non-rigid transformations; Determining the coordinates of a transformed point
Section 2.6 Mathematical Models: Constructing Functions
 What is Mathematical Modeling? (Formulate, Solve, Interpret, Test)
 Particular Examples of the Modeling (examples and problems from the section)
 Connections between an application/context and a mathematical model, Meaningful or Practical Domain
Section 3.1 Linear Functions
 Definition: A Linear Function is a function with formula description of the form L(x) = mx + b where m and b are real
numbers. The slope of a non-vertical line is the signed vertical displacement corresponding to a one unit increase in the
horizontal coordinate.
 Connection between slope positive, negative, and zero and increasing, decreasing, and constant
 Linear Functions are characterized by a constant average rate of change, i.e. Given L is a linear function, there is a real
number k so that the slope of the secant line between any two points on L is always k.
 Using this characterization to determine whether a set of points are collinear
 Applications of linear functions
Section 3.2
 Given a set of points, displaying the scatter plot (or scatter diagram) of these points (i.e. the graph)
 Given a scatter plot, having an impression of the strength of the linear relationship between the quantities
 Using technology (graphing calculator) to perform linear regression on a set of points


Intuition for linear regression: What criteria are used to find the line of best fit with linear regression?
Interpreting slope as well as coordinates of intercepts and other points in contextual application problems
Section 3.3 Quadratic Functions
 Definition: A Quadratic Function is a function with formula description of the form q(x) = ax2 + bx +c where a, b, and c are
real numbers.
 Solving quadratic equations using factoring, completing the square, and the quadratic formula
 Features of Quadratic Functions: Domain, Range, Vertex, Axis of Symmetry, Intercepts, Local Maximum or Local
Minimum, Intervals on which the quadratic function is increasing or decreasing
 Connection between the forms q(x) = ax2 + bx +c and q(x) = a(x-h)2 +k
o h = b/(2a) k = (b2-4ac)/(4a)
 Using transformation theory (Section 2.5) to obtain the graph of q(x) = a(x-h)2 +k
Section 3.4 Quadratic Models
 Finding coordinates of a point including the vertex and the intercepts
 Interpreting the coordinates of a point on the graph (serving as a model) in context
 Quadratic Regression
Section 3.5 Inequalities Involving a Quadratic Function
 First note that all such inequalities are equivalent to one of the form ax2 + bx +c < 0 or ax2 + bx +c ≤ 0
 Two standard approaches both begin by finding the horizontal intercepts (solutions to ax 2 + bx +c = 0), where these
intercepts are the finite boundaries of the interval(s) comprising the solution.
o Use the graph to determine the intervals for which the desired relationship holds
o Test the intercepts, use a test point from each interval, where these intervals are determined by the horizontal
intercepts. As there can be zero, one, or two horizontal intercepts, there can be one, two or three intervals to test
respectively i.e. the number of intervals to test exceeds the number of horizontal intercepts by exactly one.
Section 4.1 Polynomial Functions
 Definition of a polynomial function
 Given the factored form of a polynomial
o Finding the domain
o Finding the vertical intercept
o Finding zeros (horizontal intercepts) and their multiplicities
 Using knowledge of shifted power functions to determine behavior near zeros
o End behavior of the polynomial from the degree term
o Sketching the graph labeling intercepts
o Assumptions about the graph of a polynomial
 The graph is smooth, no cusps and no corners
 The graph is continuous, no holes and no breaks
 If degree is n, the graph has at most n-1 turning points
Section 4.2 and 4.3: Rational Functions
 Definition of a rational function
 Finding the domain
 Finding the vertical intercept
 Finding zeros (horizontal intercepts) and their multiplicities
o Using knowledge of shifted power functions to determine the behavior near zeros
 Determining end behavior
o Finding horizontal asymptotes (deg of numerator less than or equal to deg of denominator)
o Finding oblique/slant asymptotes using long division (deg of numerator = 1 + deg of denominator)
 Finding values not in the domain of the rational function
o Using knowledge of shifted reciprocal power functions to determine the behavior near such points
o Determining when there is a vertical asymptote
o Detecting holes in the graph
o Using knowledge of shifted reciprocal power functions to determine the behavior near points not in the domain
Section 4.4 Polynomial and Rational Inequalities
 Finding the key points (locations where the denominator or numerator is zero)
 Using these key points to partition the number line into intervals
 Using test points for each of the intervals
 Determining whether the key points should be included in the solution
 Expressing the solution in interval notation, inequality notation, as a graph on the number line
Section 5.1 Composition






Defining a composition of functions in words
Intuitive idea of "chaining" functions together
Finding the composition of functions using formula descriptions
Determining the domain of the composition
Evaluating the composition of functions at a point
Decomposing a composition into component functions
Section 5.2 Inverse Functions
 Defining Inverse of a function
 Inverse Function of a function; connection between domains and ranges of these functions
 Defining the terms one to one and one to one function
o Intuitively, one to one means no partner sharing
o Determining when a graph that represents a function is one to one; the horizontal line test
 Relationship between a one to one function and its inverse function in terms of composition
 Relationship between the graphs of a one to one function and its inverse function
 Reading the domain and range of a function from the graph
 Finding the inverse function of a one to one function using formula descriptions
 Finding the range of a one to one function by finding the domain of its inverse function
Section 5.3 Exponential Functions
 Laws of exponents; add this law ax-y = ax/ay for all positive real numbers a, and for all real numbers x and y.
 Definition of an exponential function; restrictions on the bases we consider; all have vertical intercept (0,1)
 Graphs of exponential functions: two cases (0 < a < 1 (exponential decay) ; a >1 (exponential growth))
 Transformations (scaling, reflecting, shifting) of exponential functions
 Definition of the irrational number e in terms of a limit, e is considered the natural base
 Characterization of exponential functions:
o If E(x)=ax is an exponential function, then E(d)/E(c) = ad-c for all real numbers c and d.
 Exponential functions are one to one
 Simple exponential equations – strategy: write each side as an exponential expression with the same base
Section 5.4 Logarithmic Functions
 Definition of logarithm; logarithmic form and exponential form; restrictions on the bases we consider
o Intuitively logarithm asks a question
o logb(a) asks "What power of b is a?"
 Definition of logarithmic functions; all have horizontal intercept (1,0)
 Inverse Function relationship between an exponential function and the corresponding logarithmic function
 Transformations (scaling, reflecting, shifting) of logarithmic functions
 Common logarithm (base 10; sometimes base suppressed)
 Natural logarithm (base e, usually written as ln(x))
 Simple logarithmic equations: sometimes simply rewrite using exponential form will help us solve these
Section 5.5 Properties of Logarithms
 Based on Exponential and Logarithmic Functions as Inverses (4 properties)
 Based on Rules of Exponents (3 properties) AND Change of Base Relationship
 Applying these properties (write as a single logarithm, expand to logarithms of "simple" expressions)
 Using change of base to convert to base 10 or base e supported by the technology
Section 5.6 Logarithmic and Exponential Equations
 Using Properties of Logarithms and Rules of Exponents and the facts that exponential and logarithmic functions are one to
one to find exact solutions to equations
 Using a graphing calculator to approximate a solution to an exponential or logarithmic equation
Section 5.7 Compound Interest
 Simple Interest, Compound Interest, Continuously Compound Interest
 Future Value A, Present Value P, Number of compoundings in one year n, Time of investment in years t
 Nominal Annual Interest Rate expressed as a decimal r, so for example 8.347% corresponds to r = 0.08347
 Terms for compounding frequencies: annually, semiannually, quarterly, monthly, weekly, daily
 Solving for various parameters given values for the others: Solving for A, r, t, P; Word problems
 Calculating and defining Effective Rate – comparing investments
 Doubling Time (how long to double?) and generalize -- how long will it take to grow to a given size?
6.1: Angles and Their Measure
 Be able to state and apply the definition of radian measure






Be able to convert from radians to degrees and degrees to radians
Be able to convert from degrees to degrees/minutes/seconds (DMS) and DMS to degrees
Be able to apply, define, and provide a measurement of an angle in standard position
Be able to find arc length subtended by a given angle
Be able to calculate the arc length, perimeter and area of a sector of a circle.
Be able to calculate linear and angular speeds of points on a circle/disk/wheel
6.2: Trigonometric Functions
 Be able to state and apply the definition of the six trigonometric functions
 Know the trigonometric function value and the radian measure of the good angles
o (30 degrees, 45 degrees and 60 degrees)
o as well as any angle which has a good angle as its reference angle.
 Know all the trigonometric function values and the radian measures of the quadrantal angles
o (0 degrees, 90 degrees, 180 degrees, and 270 degrees)
 Know/apply definitions of trigonometric functions in terms of circles other than the unit circle.
6.3: Properties of Trig. Functions
 Given the sine or cosine (but not both) of an angle and quadrant for its terminal side, be able to find the exact values other
five trigonometric functions of the angle.
 Given a trigonometric function value of a number and some information to determine quadrant, be able to find the exact
values other five.
 Be able to state and apply the fundamental identities
o the basic trigonometric identities (write in terms of sine and cosine)
o pythagorean identities
o periodic identities as well as the even/odd identities
 For functions y = cosx and y = sinx, know the domain, range, period and amplitude, even/odd
 For functions y = tanx, y = cotx, y = secx, y = cscx,
o know the domain, range, period and the equations of the vertical asymptotes, even/odd
6.4: Graphs of Sine and Cosine
 For functions y = Acos(Bx), y = Asin(Bx), be able to
o graph the function over any subset of its domain
o sketch a graph labeling all maxima, minima, and horizontal intercepts (if any) and vertical intercept (if any) with
their EXACT coordinates over any subset of the domain
o find an equation for a given graph
6.5: Graphs of Tangent, Secant, Cosecant, Cotangent Functions
 For functions y = Acot(Bx+C), y = Atan(Bx+C), y = Acsc(Bx+C), and y = Asec(Bx+C), be able to
o find the domain and range
o sketch a graph labeling all of the horizontal intercepts (if any) and vertical intercept (if any) with their EXACT
coordinates over any subset of the domain
o label all vertical asymptotes with their exact equations over any subset of the domain
6.6: Phase Shift, Sinusoidal Curve Fitting
 For functions y = Acos(Bx+C), y = Asin(Bx+C) be able to find the domain and range as well as sketch a graph labeling all
maxima, minima, and horizontal intercepts (if any) and vertical intercept (if any) with their EXACT coordinates over any
subset of the domain
 Approximation of a curve of the form y = Asin(Bx+C)+D to sinusoidal data and Sinusoidal Regression
7.1: Inverse Sine, Cosine and Tangent Functions
 Graphs of inverse sine, inverse cosine and inverse tangent functions and finding exact values of inverse sine, inverse cosine
and inverse tangent functions and compositions with standard trig. functions
7.2: Inverse Secant, Cosecant and Cotangent Functions
 Graphs of inverse sine, inverse cosine and inverse tangent functions and finding exact values of inverse sine, inverse cosine
and inverse tangent functions and compositions with standard trig. functions
7.3: Trigonometric Identities
 Definition of an identity, definition of a conditional equation
 The Basic Identities
 Deriving/Establishing identities (providing reasons/justifications for steps in the derivation)
 Guidelines for deriving trigonometric identities
2.1 in text: 15, 19, 33, 39, 51, 61, 73, 87
others: 17, 21, 23, 25, 43, 45, 47, 49, 55, 57, 65, 71, 77, 79, 85, 91, 95, 99
2.2 in text: 9, 13, 15, 25, 31
others: 11, 17, 19, 21, 27, 37, 46
2.3 in text: 11, 13, 15, 17, 19, 21, 33, 45, 53, 59
others: 22, 23, 25, 29, 31, 35, 37, 39, 55, 57, 61, 63, 81, 85
2.4 in text: 9-16, 29
others: 19, 23, 25, 31, 33, 37, 41, 43, 45, 47, 49, 55, 67
2.5 in text: 27, 35, 39, 41, 43, 57, 65
others: 7-18(all), 19, 21, 23, 25, 29, 31, 33, 37, 49, 53, 55, 59, 67
2.6 in text: 1, 7
others: 3, 5, 9, 11, 15, 19, 23
3.1 in text: 13, 21, 41, 47
others: 15, 17, 19, 23, 24, 27, 31, 33, 37, 43, 49, 51, 53
3.2 in text: 3, 9
others: 5, 7, 15, 17, 19, 21
3.3 in text: 27, 35, 43, 47, 53
others: 21, 29, 31, 33, 37, 41, 45, 51, 55, 57, 59, 65, 85
3.4 in text: 3, 7, 11, 13, 27
others: 5, 9, 15, 17, 19, 29
3.5 in text: 5, 9, 13
others: 3, 7, 15, 17, 23, 27, 31, 33, 35
4.1 in text: 11, 15, 23, 29, 37, 45, 57, 63, 67, 77, 89
others: 13, 17, 19, 51, 55, 69, 79, 87
4.2 in text: 13, 23, 31, 41, 43, 45
others: 11, 15, 19, 21, 25, 27, 47, 50 (Answer: HA: y =2; VA: x = 2, VA: x = -1/3), 51
4.3 in text: 7, 13, 15, 33, 45, 55
others: 9, 21, 25, 31, 47, 51
4.4 in text: 5, 13, 17, 21, 29
others: 9, 15, 19, 25, 33, 37, 43, 45
5.1 in text: 11, 21, 33, 35, 45, 53
others: 7, 15, 17, 19, 23, 25, 27, 37, 41, 47, 49, 51, 55, 57, 59, 61
5.2 in text: 9, 13, 17, 23, 27, 31, 41, 63
others: 11, 15, 19, 21, 33, 35, 37, 39, 43, 45, 51, 53, 57, 61, 65, 71, 73, 75
5.3 in text: 11, 21, 37, 49, 59
others: 23, 27, 29, 31, 33, 35, 39, 41, 45, 63, 65, 67, 69, 71, 75, 83, 85, 87, 89, 111, 113
5.4 in text: 9, 17, 25, 39, 45, 59, 71, 79, 87, 99
others: 11, 13, 15, 19, 21, 23, 27, 29, 31, 33, 35, 37, 43, 47, 57, 77, 89, 91, 93, 97, 101, 103, 105
5.5 in text: 9, 13, 17, 45, 51, 65, 73
others: 7, 11, 15, 19, 21, 23, 25, 27, 29, 35, 41, 47, 49, 53, 57, 59, 63, 67, 69, 71
5.6 in text: 13, 21, 31, 35, 45, 53, 63
others: 9, 15, 17, 25, 29, 37, 41, 43, 49, 51, 55, 75, 79, 81, 85, 87
5.7 in text: 3, 11, 13, 27, 31, 35
others: 5, 7, 17, 19, 23, 25, 39, 41, 43, 45, 47, 49
6.1 in text: 11, 23, 29, 35, 47, 61, 71, 79, 97, 101
others: 13, 15, 17,19, 21, 25, 27, 31, 33, 37, 39, 41, 43, 45, 49, 51, 53, 55, 57, 59, 63, 65, 67, 69, 73, 75, 77, 81, 83, 87, 89, 91, 93, 95, 99, 107
6.2 in text: 11, 19, 33, 39, 49, 53, 57, 63, 67, 83
others: 13, 17, 21, 23, 25, 27, 29, 31, 35, 37, 41, 43, 45, 47, 51, 55, 59, 61, 65, 69, 77, 85, 89, 91, 93, 123
6.3 in text: 11, 27, 35, 43, 59, 79, 97
others: 13, 19, 29, 31, 33, 37, 41, 45, 47, 53, 55, 57, 61, 69, 77, 81, 85, 89, 91, 93, 94, 115
6.4 in text: 9, 11, 13, 23, 45, 49, 53, 59, 67, 71
others: 15, 17, 19, 25, 27, 33, 35, 51, 61, 65, 73, 75, 77, 79, 89, 91
6.5 in text: 7, 15, 21, 23, 29
others: 9, 11, 13, 17, 27, 35, 37, 43, 45, 47, 49
6.6 in text: 3, 29, 35
others: 3, 5, 7, 9, 11, 13, 19, 25, 31
7.1 in text: 13, 17, 19, 23, 25, 37, 41, 43, 45, 49, 55, 61
others: 15, 47, 51, 59, 63, 65, 67
7.2 in text: 9, 27, 39, 45, 57
others: 11, 13, 15, 17, 19, 21, 23, 25, 29, 31, 33, 35, 37, 41, 43, 59, 63
7.3 in text: 9, 11, 13, 19, 23, 27, 49, 53, 69
others: 21, 37, 39, 47, 55, 65, 73, 77, 81, 87, 93, 95, 97
Properties, Formulas, and Facts
Properties of Exponents
For all positive real numbers a and b and for all real numbers s and t:
(E1) asat = as+t
(E2) (as)t = ast
(E3) asbs = (ab)s
(E4) a-s = 1/(as) = (1/a) s
(E5) 1s = 1
(E6) a0 = 1
(E7) as/at = as-t
(E8) as/bs = (a/b)s
Properties of Logarithms
For all positive real numbers a and b such that a ≠ 1 and b ≠ 1 and for all positive real numbers
M and N and for all real numbers r:
(L1) logb(br) = r
(L2) blogb(M) = M
(L3) logb(b) = 1
(L4) logb(1) = 0
(L5) logb(MN) = logb(M) + logb(N)
(L6) logb(M/N) = logb(M)  logb(N)
(L7) logb(Mr) = r logb(M)
(L8) logb(M) = loga(M)/ loga(b)
Banking Problems
(B1) A = P + Prt
(B2) A = P(1+ r/n)nt
(B3) A = Pert
Other Facts
(F1) For all real numbers x and y and all positive real numbers a satisfying a ≠ 1,
if x = y, then ax = ay
(F2) For all real numbers x and y and all positive real numbers a satisfying a ≠ 1,
if ax = ay then x = y.
(F3) For all positive real numbers x and y and all positive real numbers b satisfying b ≠ 1,
if logb(x) = logb(y) then x= y
(F4) For all positive real numbers x and y and all positive real numbers b satisfying b ≠ 1,
if x= y then logb(x) = logb(y)