* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Discussion7
Mechanical filter wikipedia , lookup
Crystal radio wikipedia , lookup
Surge protector wikipedia , lookup
Operational amplifier wikipedia , lookup
Integrated circuit wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Distributed element filter wikipedia , lookup
Power electronics wikipedia , lookup
Audio crossover wikipedia , lookup
Flexible electronics wikipedia , lookup
Opto-isolator wikipedia , lookup
Regenerative circuit wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Phase-locked loop wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Electronic engineering wikipedia , lookup
Nominal impedance wikipedia , lookup
Equalization (audio) wikipedia , lookup
Standing wave ratio wikipedia , lookup
Rectiverter wikipedia , lookup
Index of electronics articles wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Zobel network wikipedia , lookup
Radio transmitter design wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
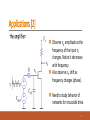
Discussion 7 CLASS X NOV. XX Overview Phasors in Electrical Engineering (EE) Phasors ⇌ Sinusoid Circuit Models in Frequency Domain Generalized Circuit Analysis 1 Phasors in Electrical Engineering (EE) Why phasors are useful in EE? It is a long story… Any practical periodic function can be represented as sum of sinusoids (FT) For LTI system, sinusoids input results in sinusoids outputs Phasors can perfectly represent sinusoids mathematically and what’s more, they can simplify the computation With the help of phasors, DC circuit analysis methods can be generalized to AC circuits 2 Motivation for Using Phasors A voltage source 5cos(6t) is connected in series with a 4Ω resistor and a 0.5H inductor. Compute the current i(t) which flows through all three devices. [1] di 0.5 dt Hard Way 1. KVL: 5 cos 6t = 4i + (1) 2. the trial solution is i(t) = A cos(6t) + B sin(6t) (2) 3. Substituting (2) to (1) gives [5−4A−3B]cos(6t)+[−4B+3A]sin(6t)=0 4. Set t = 0 and t = π, solving 5 = 4A + 3B and 0 = 3A − 4B. 5. A = 0.8 and B = 0.6, i(t) = 0.8 cos(6t) + 0.6 sin(6t) 6. i(t) = cos(6𝑡 − 37° ) 3 Motivation for Using Phasors A voltage source 5cos(6t) is connected in series with a 4Ω resistor and a 0.5H inductor. Compute the current i(t) which flows through all three devices. ° 5 5 −𝑗37 Easy Way 1. Phasor 𝐼 = = 1𝑒 1 = 4+𝑗6∗ 2 4+𝑗3 2. 𝑖 𝑡 = cos(6𝑡 − 37° ) Remark Complex number help us simplify the computation. You do not need to solve differential equations in AC circuits any more! 4 Phasors ⇌ Sinusoid* Phasor can perfectly represent sinusiod in the following aspects : A sinusiod function can be transformed to a phasor, and they are totally equivalent mathematically Sinusiod related operations can be replaced by corresponding phasor operations *: “⇌” means “equivalent to” here; the left/right side can represent each other. 5 Euler’s Identity 𝒆±𝒋𝒛 = 𝐬𝐢𝐧 𝒛 ± 𝒋 𝐜𝐨𝐬 𝒛 Resulting in cos 𝒛 = 𝒆𝒋𝒛 +𝒆−𝒋𝒛 , 𝟐 sin 𝒛 = 𝒆𝒋𝒛 −𝒆−𝒋𝒛 𝟐𝒋 A sinusiod function can be equivalently transformed to a phasor: 𝑣 𝑡 = 𝑉𝑚 cos(𝜔𝑡 + 𝜙) ⟺ 𝐕 = 𝑉𝑚 ∠𝜙 Remark Frequency is separated from 𝑣 𝑡 by the transformation, which remains unchanged in a LTI system once given from input. 6 Algebraic Operations Complex sinusiod related operations can be replaced by corresponding simple phasor operations: Complex operations in time domain A cos(𝜔𝑡 + 𝜑1 ) + B sin(𝜔𝑡 + 𝜑2 ) 𝑑𝑣 Differentiation: 𝑑𝑡 Integration: 𝑣𝑑𝑡 Simple operations in phasor domain ⟺ A∠𝜑1 + B∠(𝜑2 − 90° ) ⟺ Multiplication: 𝑗𝜔𝐕 𝐕 ⟺ Division: 𝑗𝜔 7 Impedance Model in Phasor Domain The current through the capacitor will increase with higher frequency, even if the voltage amplitude stays constant. It takes a higher voltage to push the same current amplitude through an inductor at higher frequency. Just the same as in time domain. 8 Impedance Model in Phasor Domain Remarks The impedance of any circuit element is two numbers, a magnitude and a phase, at every frequency value. Both the magnitude and the phase may be frequency dependent. When we describe the impedance, we need to specify at what frequency we are describing the impedance. 9 AC Circuits Analysis Steps to analyze AC circuits: 1. Transform the circuit to the phasor 2. Solve the problem using: KCL/KVL in frequency domain Series/Parallel Impedance Combinations/∆-Y Trans. Nodal/Mesh Analysis Superposition Theorem Source Transformation Thevenin/Norton Equivalent Circuits 3. Transform the results in frequency domain to the time domain 10 Transient vs. Steady-State Analysis Sinusoid steady-state analysis: solve steady-state (t → ∞) response which contains purely sinusoidal, without the transient exponential terms which decays to 0 as t → ∞. 11 Applications Did you ever buy audio equipment, like microphone? If you looked at the specifications for audio equipment you would probably find the following: If the unit is a speaker set, you'll find separate frequency responses for the different speakers like the mid-range, or the woofer and the tweeter. If the unit is a microphone, you'll find a frequency response that tells you how the unit responds to different frequencies. 12 Applications Given a linear system or circuit described mathematically, Be able to compute a frequency response for the system Be able to predict an output signal from a given input sinusoidal signal 13 Applications [2] Observe 𝑣𝑜 amplitude as the frequency of the input 𝑣𝑖 changes. Notice it decreases with frequency. Also observe 𝑣𝑜 shift as frequency changes (phase). Need to study behavior of networks for sinusoidal drive. 14 Exercise 1 1. Determine the currents 𝑖1 (𝑡), 𝑖2 𝑡 and 𝑖3 (𝑡) using impedance combination, nodal and mesh analysis. 15 Exercise 1 - Impedance Combination 16 Exercise 1 - Nodal Analysis 17 Exercise 1 - Mesh Analysis 18 Exercise 2 2. Determine the Thevenin and Notton equivalent circuit for the circuit below, assuming that 𝜔 = 104 rad/s. 19 Exercise 2 – Thevenin Equivalent 20 Exercise 2 – Norton Equivalent 21 Some After-Class Questions for you When capacitors or inductors used in AC circuits, is the current and voltage peak at the same time? Why or why not? In a linear system, does the frequency of a sinusoid convey information? Can phasor analysis be performed on multiple frequencies circuits? 22 Some After-Class Questions for you Phasor analysis gives the transient response or steady-state response? What's the physical meaning of the imaginary component of impedance? Find an intuitive instance, and explain to a high school student why do we need frequency domain analysis. 23 Q&A 24 REFERENCES [1] COMPLEX NUMBERS AND PHASORS, Professor Andrew E. Yagle, EECS 206 Instructor, Fall 2005, Dept. of EECS, The University of Michigan, Ann Arbor, MI 48109-2122 [2] Anant Agarwal and Jeffrey Lang, course materials for 6.002 Circuits and Electronics, Spring 2007. MIT OpenCourseWare, Massachusetts Institute of Technology. 25