Download Understanding the destruction of nth

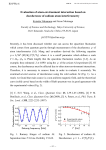
PHYSICAL REVIEW A 66, 012112 共2002兲
Understanding the destruction of nth-order quantum coherence in terms of multipath interference
D. L. Zhou,1,2 P. Zhang,2 and C. P. Sun2,*
1
Center for Advanced Study, Tsinghua University, Beijing 100084, China
Institute of Theoretical Physics, Academia Sinica, P.O. Box 2735, Beijing 100080, China
共Received 11 June 2001; revised manuscript received 15 March 2002; published 30 July 2002兲
2
The classic example of the destruction of interference fringes in a ‘‘which-way’’ experiment, caused by an
environmental interaction, may be viewed as the destruction of first-order coherence as defined by Glauber
many years ago 关Phys. Rev. 130, 2529 共1963兲; 131, 2766 共1963兲兴. However, the influence of an environment
can also destroy the nth-order quantum coherence in a quantum system, where this high order coherence is
captured. We refer to this phenomenon as the nth-order decoherence. In this paper we show that, just as the
first-order coherence can be understood as the interference of the amplitudes for two distinct paths, the higher
order coherence may be understood as the interference of multiple amplitudes corresponding to multiple paths.
To see this, we introduce the concept of nth-order ‘‘multiparticle wave amplitude.’’ It turns out that the
nth-order correlation function can be expressed as the square norm of some multiparticle wave amplitude for
the closed system or as the sum of such square norms for the open system. We also examine, as a specific
example, how an environment can destroy the second-order coherence by eliminating the interference between
various multiple paths.
DOI: 10.1103/PhysRevA.66.012112
PACS number共s兲: 03.65.Yz, 32.80.⫺t, 42.50.⫺p
I. INTRODUCTION
A most profound concept in quantum physics is quantum
coherence. The first-order version of quantum coherence can
be directly manifested by the superposition of two quantum
states. This is quite similar to the optical coherence in
Young’s double slit experiment. From the standpoint of the
photon-detection theory of Glauber, this simple coherence
can be mathematically depicted by the first-order correlation
function 关1兴. However, in quantum mechanics, this first-order
coherence phenomenon does not sound very marvellous
since the same circumstance can also occur in a classical
case, such as the optical interference in the above mentioned
Young’s double-slit experiment. In fact, by first-order correlation function only, it is impossible to distinguish the nature
of a laser light field and a conventional light field with identical spectral properties. As an effective remedy, Glauber’s
nth-order quantum correlation function, which accounts for
various intrinsic (nth-order兲 quantum coherence effects, such
as the intensity-intensity correlation measurement in the
Hanbury-Brown-Twiss experiment 关2兴, was introduced 关1兴.
Indeed, this function reflects the intrinsically quantum features of coherence beyond the classical analog.
Quantum coherence embodies the wave nature in the
world of microscopic particles. On the other hand, it is very
fragile and can easily be destroyed by a ‘‘which-path共way兲’’
experiment 关3,4兴, or by an environmental interaction. This
phenomenon of destruction of coherence is usually referred
to as quantum decoherence 关5,6兴. The phenomenon of losing
coherence described by the first-order correlation function is
defined as first-order quantum decoherence. Motivated by
considerations of the fundamental quantum measurement
*Electronic
address:
www.itp.ac.cn/ ~suncp
[email protected];
1050-2947/2002/66共1兲/012112共9兲/$20.00
URL:
http://
problem 关7,8兴 , and also by the attempts to preserve quantum
coherence of qubits in quantum computing 关9–11兴, many
recent experimental and theoretical investigations have been
focused on revealing the physical mechanism of the decoherence problem, e.g., see 关12兴. According to these studies, this
first-order decoherence can be roughly understood through
the quantum entanglement of the considered system with the
environment or the measuring apparatus.
Obviously, this entanglement implies a ‘‘whichpath共way兲’’ detection 关3兴 in the single particle picture. Precisely speaking, in an initial coherent superposition 兩 ␺ s 典
⫽ 兺 c n 兩 n 典 , each system state 兩 n 典 corresponds to a ‘‘path’’ and
many ‘‘two-path’’ interferences are reflected in the square
norm of the spatial wave function 具 x 兩 ␺ s 典 . Thus by considering 具 x 兩 ␺ s 典 the quantum coherence can be captured to some
extent. After the interaction, each ‘‘path’’ is correlated with
an environment state 兩 e n 典 to form an entangling state 兩 ␺ T 典
⫽ 兺 c n 兩 n 典 丢 兩 e n 典 . Here, the different states 兩 e n 典 distinguish
among the ‘‘paths’’ of different 兩 n 典 and thus record the information of each ‘‘path.’’ The interference terms in the spatial intensity I(x)⫽Tr( 具 x 兩 ␺ T 典具 ␺ T 兩 x 典 ) will disappear when
the environment states 兩 e n 典 are completely distinct, i.e.,
具 e m 兩 e n 典 ⫽ ␦ mn . In that case each path is labeled by an environment state.
The above well-known explanation of the first-order decoherence in terms of a ‘‘which-path共way兲’’ detection
mechanism is simple but very profound. However, it is not
yet clear whether this mechanism can be used to elucidate
nth-order quantum decoherence (n-QDC兲, the destruction of
quantum coherence described by Glauber’s nth-order correlation function. The difficulty is we do not exactly know
what are the ‘‘paths’’ and the corresponding ‘‘which-path’’
detection. Most recently, we have touched on the secondorder quantum decoherence problem 关13兴, bypassing this difficulty. As a matter of fact, in our treatment, we did not
define the concept of ‘‘path’’ directly. The concrete calcula-
66 012112-1
©2002 The American Physical Society
PHYSICAL REVIEW A 66, 012112 共2002兲
D. L. ZHOU, P. ZHANG, AND C. P. SUN
tion in Ref. 关13兴 motivated us to consider the ‘‘which-path’’
picture of higher order quantum decoherence in general.
In our present investigation, we notice that, for a closed
system, in some cases Glauber’s nth-order correlation function is the square norm of the nth-order ‘‘multiparticle wave
amplitude,’’ which will be defined later in this paper, while
for an open system, it can become the sum of the square
norms of the nth-order multiparticle wave amplitude over the
states of an environment or an apparatus interacting with this
open system. This observation is crucial in our present investigation. As an effective wave function, this multiparticle amplitude can be shown to be a supposition of many generalized ‘‘paths’’ 共the multiparticle paths or simply multiple
paths兲. Thus, the higher order coherence may be understood
as the interference of multiple particle amplitudes. With this
conception a generalized ‘‘which-path’’ detection may be established in terms of multiparticle paths as the physical
mechanism of higher order decoherence for some examples.
In Sec. II, we will briefly explain Glauber’s nth-order
quantum coherence in terms of the single- and multiphoton
effective wave functions used in 关14,15兴. As their generalizations, in Sec. III the concepts of multiparticle path and
multiparticle wave amplitude are introduced for both closed
and open bosonic systems. In particular, the nth-order correlation functions of bosonic systems are studied. In Sec. IV,
an intracavity model with two bosonic modes is used to demonstrate 2-QDC as a ‘‘which-path’’ detecting process. In Sec.
V, the exact solution obtained in the Appendix is utilized to
show the dynamical process of 2-QDC, which is caused by
entanglement with the environment or an apparatus and indeed can be explained as a generalized ‘‘which-path’’ measurement for explicitly defined multiparticle paths.
II. THE nTH-ORDER COHERENCE FOR QUANTIZED
LIGHT FIELD AND MULTIPHOTON
WAVE AMPLITUDE
In quantum mechanics, a pure state is a superposition
兩 ␺ 典 ⫽ 兺 k c k 兩 k 典 of many components 兩 k 典 , but the corresponding mixture ␳ ⫽ 兺 k 兩 c k 兩 2 兩 k 典具 k 兩 can describe the same classical
probability distribution 兩 c k 兩 2 . However, 兩 ␺ 典 and ␳ represent
different quantum realities. Usually it is said that the two
components of a pure state are more coherent than those of a
mixed one. This coherence property is obviously reflected by
the intensity interference of two ‘‘paths’’ corresponding to
the two components in the quantum state. For a system of
one particle, only the single-particle property is relevant for
this observation. In this sense, only an intensity interference
experiment is essential for a one-particle system. For a
many-particle system, however, there exist many experiments 共such as the Hanbury-Brown-Twiss experiment and
the intensity-intensity correlation measurement兲 to show the
much richer nature of quantum coherence.
In order to study quantum coherence in a many-particle
system, Glauber introduced the so-called nth-order quantum
correlation function (n-QCF兲
G (n) 共 ␣ 1 ,t 1 ; ␣ 2 ,t 2 ; . . . ; ␣ n ,t n 兲 ⫽Tr 关 ␳ˆ E ␣† 共 t 1 兲 E ␣† 共 t 2 兲 •••E ␣† 共 t n 兲 E ␣ n 共 t n 兲 •••E ␣ 2 共 t 2 兲 E ␣ 1 共 t 1 兲兴 ,
1
2
n
共1兲
for the electromagnetic field E ␣ (t) in different modes ␣ . Here, E ␣ (t) is the annihilation operator of mode ␣ at time t in the
Heisenberg picture, E ␣† (t) is the corresponding conjugate operator, and the density matrix ␳ˆ represents the initial state of the
many-mode electromagnetic field. Of course, this formalism can also be used to study the coherence property for any quantum
many-body system.
Furthermore, to describe the higher order coherence, Glauber also defined the nth-order coherence function in the form 关16兴
g ␣␤ ⬅g 共 ␣ 1 , ␣ 2 , . . . , ␣ n ; ␤ 1 , ␤ 2 , . . . , ␤ n 兲 ⫽
Tr 关 ␳ˆ E ␤† 共 t 1 兲 E ␤† 共 t 2 兲 •••E ␤† 共 t n 兲 E ␣ n 共 t n 兲 •••E ␣ 2 共 t 2 兲 E ␣ 1 共 t 1 兲兴
1
2
n
冑G 关 ␣ 1 ,t 1 ; ␣ 2 ,t 2 ; . . . ; ␣ n ,t n 兴 冑G 关 ␤ 1 ,t 1 ; ␤ 2 ,t 2 ; . . . ; ␤ n ,t n 兴
Obviously, this coherence function is defined by the ratio of
the off-diagonal elements of the reduced multitime density
matrix g⫽„g ␣␤ : ␣ ⫽( ␣ 1 , ␣ 2 , . . . , ␣ ), ␤ ⫽( ␤ 1 , ␤ 2 , . . . , ␤ n )…
to its diagonal ones. It is easily observed from this definition
that these off-diagonal elements represent the coherence effect, and each g ␣␤ correlates two diagonal elements g ␣␣ and
g ␤␤ . Thus, we can understand the coherence function as
measuring the degree of coherence for the two diagonal elements, which correspond to two different ‘‘paths.’’ From this
point of view, there is obviously no quantum coherence for a
completely mixed state with vanishing off-diagonal elements. In the following discussion, we will give simple examples to illustrate this viewpoint.
.
共2兲
Now let us turn to an instance 关14兴 from which we can see
clearly how the higher order quantum coherence effects
given by 2-QCF are revealed in the multiparticle picture.
For a single photon, the coherent superposition 兩 s 典
⫽(1/冑2)( 兩 1 k 典 ⫹ 兩 1 ⫺k 典 ) of two states with opposite wave
vectors k and k ⬘ possesses first-order quantum coherence,
which can be described by the interference fringes
G (1) 共 r,r,t 兲 ⫽ 具 s 兩 E ⫺ 共 r,t 兲 E ⫹ 共 r,t 兲 兩 s 典
⫽円具 0 兩 E ⫹ 共 r,t 兲 兩 s 典 円2 ⬀cos2 共 kr 兲 ,
where
012112-2
共3兲
PHYSICAL REVIEW A 66, 012112 共2002兲
UNDERSTANDING THE DESTRUCTION OF nTH-ORDER . . .
E ⫹ 共 r,t 兲 ⫽
兺 E k a k exp共 ikr⫺i ␻ k t 兲
is the photon field operator with positive frequency for the
annihilation operator a k . It should be noticed that the diagonal element G (1) (r,r,t) of the first-order correlation function is just the square norm of the single-photon wave packet
关15兴
具 0 兩 E ⫹ 共 r,t 兲 兩 s 典 ⫽
⫽
1
冑2
1
冑2
兵 具 0 兩 E ⫹ 共 r,t 兲 兩 1 k 典 ⫹ 具 0 兩 E ⫹ 共 r,t 兲 兩 1 k 典 其
共 E k e ikr⫺i ␻ k t ⫹E ⫺k e ⫺ikr⫺i ␻ ⫺k t 兲 .
共4兲
Therefore, G (1) (r,r,t) represents the interference between
the ‘‘two paths’’ 具 0 兩 E ⫹ (r,t) 兩 1 k 典 and 具 0 兩 E ⫹ (r,t) 兩 1 k 典 . This
just develops the corresponding concept in Young’s double
experiment for a quantized light field. The above reformulation of the first-order quantum coherence implies that ‘‘two
paths’’ are necessary for the interference phenomenon.
If we consider the two-particle state 兩 1 k ,1k ⬘ 典 with a single
component, an interesting situation arises where the firstorder quantum coherence does not appear, but we can see the
second-order effect through the second-order quantum correlation function
G (2) 共 r 1 ,r 2 ,t 1 ,t 2 兲 ⫽2E 4k 兵 1⫹cos关共 k⫺k ⬘ 兲共 r 1 ⫺r 2 兲兴 其 .
共5兲
Unlike the case of first-order coherence, in this case there do
not appear the obvious two or many ‘‘paths.’’ Nevertheless,
the interference phenomenon can still be captured in a similar way with the introduction of a generalized ‘‘path.’’ We
understand the generalized path as described by the two-time
correlation function G (2) (r 1 ,r 2 ,t 1 ,t 2 ) ⫽ 兩 ␺ 兩 2 where ␺ is the
two-photon wave function
⫹
ample of second-order coherence shows that the concept of
two-path interference in the single-photon picture still works
with a proper generalization of the concept of ‘‘path.’’ Hence
it is quite natural to seek a generalized which-path共way兲
measurement as the mechanism of higher order quantum decoherence.
III. MULTIPARTICLE AMPLITUDE FOR FREE BOSONS
In this section the conception of the two-photon effective
wave function is generalized. It is applied to a study of general quantum systems of identical particles. We first discuss
the spatially homogeneous case for the sake of simplicity.
We consider a homogeneous bosonic field with two
modes 兩 V 典 and 兩 H 典 . The generalized field operator in the
time domain,
␾ˆ 共 t 兲 ⫽c V b̂ V e ⫺i ␻ V t ⫹c H b̂ H e ⫺i ␻ H t
⬅c V 共 t 兲 b̂ V ⫹c H 共 t 兲 b̂ H ,
is an annihilation operator with respect to the superposition
state
*兩 H 典 .
兩 ⫹ 典 ⫽c V* 兩 V 典 ⫹c H
⫽E 2k e ⫺2i ␻ k t 关 e ikr 1 ⫹ik ⬘ r 2 ⫹e ik ⬘ r 1 ⫹ikr 2 兴 .
ˆ †共 t 1 兲 ␾
ˆ †共 t 2 兲 ␾
ˆ 共 t2兲␾
ˆ 共 t 1 兲 兩 1 V ,1H 典
G (2) ⫽ 具 1 V 1 H 兩 ␾
ˆ 共 t2兲␾
ˆ 共 t 1 兲 兩 1 V ,1H 典 兩 2 ⬅ 兩 ⌿ 共 t 1 ,t 2 兲 兩 2 .
⫽ 兩 具 0,0兩 ␾
共9兲
The two-time wave function
共6兲
␺ was invoked as a two-photon effective wave function, and
it was also called the biphoton wave packet for the photon
field E ⫹ (r,t) 关15兴. In particular, we remark that the biphoton
wave packet ␺ is a coherent superposition of two probability
amplitudes corresponding to two two-photon paths:
ˆ 共 t2兲␾
ˆ 共 t 1 兲 兩 1 V ,1H 典
⌿ 共 t 1 ,t 2 兲 ⫽ 具 0,0兩 ␾
can be understood in terms of the two-paths picture from the
initial state 兩 1 V ,1H 典 to the final state 兩 0,0典 :
兩 1 V ,1H 典
具 00兩 E ⫹ 共 r 2 ,t 2 兲 兩 0 k ,1k ⬘ 典具 0 k ,1k ⬘ 兩 E ⫹ 共 r 1 ,t 1 兲 兩 1 k ,1k ⬘ 典
c H共 t 1 兲
→
兩 1 V ,0H 典
c V共 t 1 兲
c 共t2兲
V
→
兩 0,0典
c H共 t 2 兲
&
and
⫹
共8兲
Here, b H and b V are the annihilation operators of the boson
system; c V and c H satisfy the normalization relation 兩 c V 兩 2
⫹ 兩 c H 兩 2 ⫽1. Without loss of generality, we take c V ⫽c H
⫽1/冑2. This means we consider the measurement to detect
the polarized boson along the 45° direction in the V-H plane.
ˆ a ‘‘measuring’’ operator.
We call ␾
ˆ , the generalized second-order correCorresponding to ␾
lation function 关13兴
⫹
␺ ⬅ ␺ 共 r 1 ,r 2 ,t 1 ,t 2 兲 ⫽ 具 00兩 E 共 r 2 ,t 2 兲 E 共 r 1 ,t 1 兲 兩 1 k ,1k ⬘ 典
共7兲
%
兩 0 V ,1H 典
⫹
具 00兩 E 共 r 2 ,t 2 兲 兩 1 k ,0k ⬘ 典具 1 k ,0k ⬘ 兩 E 共 r 1 ,t 1 兲 兩 1 k ,1k ⬘ 典 .
Starting from Glauber’s standpoint and proceeding
along, we come to the conclusion that a set
兵 G (n) ( ␣ 1 ,t 1 ; ␣ 2 ,t 2 ; . . . ; ␣ n ,t n ) 兩 n⫽1,2, . . . 其 of correlation
functions, rather than a single one, is indispensable to describe comprehensively the wave-particle dual nature in the
quantum world of many-particle systems. The above ex-
The two paths are just associated with the two amplitudes,
forming a coherent superposition,
⌿ 共 t 1 ,t 2 兲 ⫽c V c H exp共 ⫺i ␻ V t 2 ⫺i ␻ H 兲
⫹c H c V exp共 ⫺i ␻ H t 2 ⫺i ␻ V t 1 兲 .
共10兲
Correspondingly, the second-order correlation function is
012112-3
PHYSICAL REVIEW A 66, 012112 共2002兲
D. L. ZHOU, P. ZHANG, AND C. P. SUN
G (2) ⫽2 兩 c V c H 兩 2 兵 1⫹cos关共 ␻ V ⫺ ␻ H 兲共 t 2 ⫺t 1 兲兴 其 .
共11兲
ˆ †共 t 1 兲 ␾
ˆ †共 t 2 兲 ␾
ˆ †共 t 3 兲 ␾
ˆ 共 t3兲␾
ˆ 共 t2兲␾
ˆ 共 t 1 兲 兩 2 V ,1H 典
G (3) ⫽ 具 2 V 1 H 兩 ␾
The above discussion for second-order quantum coherence is applicable to the higher order case. Our arguments in
this paper are based on two observations. 共a兲 The generalized
ˆ ⫽ 兺 c n b̂ n is specified for a quantum measurefield operator ␾
ment about a superposition single-particle state 兩 ␾ 典
⫽兺c*
n 兩 n 典 . 共b兲 For a certain initial single-component state
兩 s 0 典 of an N-particle system, the nth-order quantum correlation function
G (n) 共 r 1 ,r 2 , . . . ,r n ,t 1 ,t 2 , . . . ,t n 兲 ⫽ 兩 ␺ (n) 兩 2
ˆ 共 t3兲␾
ˆ 共 t2兲␾
ˆ 共 t 1 兲 兩 2 V ,1H 典 兩 2
⫽ 兩 具 0,0兩 ␾
⬅ 兩 ⌿ 共 t 1 ,t 2 ,t 3 兲 兩 2
is a norm square of the two-time wave function
ˆ 共 t3兲␾
ˆ 共 t2兲␾
ˆ 共 t 1 兲 兩 2 V ,1H 典
⌿ 共 t 1 ,t 2 ,t 3 兲 ⫽ 具 0,0兩 ␾
⫽ 冑2c V2 c H e ⫺i ␻ V (t 3 ⫹t 2 )⫺i ␻ H t 1
共12兲
⫹ 冑2c H c V2 e ⫺i ␻ H t 2 ⫺i ␻ V (t 3 ⫹t 1 )
⫹ 冑2c H c V2 e ⫺i ␻ H t 3 ⫺i ␻ V (t 2 ⫹t 1 ) .
can be written as the norm square of an effective wave function ␺ (n) , which is just a superposition of many amplitudes.
Let us consider the third-order situation as an example.
Let the initial state be 兩 1 H ,2V 典 . Then the generalized thirdorder correlation function
兩 2 V ,0H 典
共14兲
Each term in the above effective wave function is contributed by the corresponding one of the four paths from 兩 2 V ,1H 典
to 兩 0,0典 :
c 共t2兲
V
→
兩 1 V ,0H 典
c H共 t 1 兲
c V共 t 3 兲
%
&
c 共t1兲
兩 2 V ,1H 典
共13兲
V
→
兩 1 V ,1H 典
c H共 t 2 兲
→
兩 1 V ,0H 典
c V共 t 2 兲
c V共 t 3 兲
→
兩 0,0典
c H共 t 3 兲
&
%
兩 0 V ,1H 典
In terms of the effective three-time wave function defined
above, the third-order correlation function is explicitly written down:
G (3) ⫽4 兩 c V2 c H 兩 2
冉
3
⫹cos关共 ␻ V ⫺ ␻ H 兲共 t 2 ⫺t 1 兲兴
2
⫹cos关共 ␻ V ⫺ ␻ H 兲共 t 3 ⫺t 1 兲兴
ˆ 共 0 兲 U 共 t,0兲
B̂ 共 t 兲 ⫽U † 共 t,0兲 ␾
ˆ 共 t 兲 exp共 ⫺iV̂t 兲 ,
⫽exp共 iV̂t 兲 ␾
共15兲
ˆ (0)⫽c V b̂ V ⫹c H b̂ H has been given by Eq. 共7兲. Then
where ␾
instead of the free time evolution governed by the free
Hamiltonian H 0 , we use the evolution operator U(t,0) governed by the total Hamiltonian
冊
⫹cos关共 ␻ V ⫺ ␻ H 兲共 t 2 ⫺t 3 兲兴 .
H⫽H 0 ⫹W⫹H E ⬅H 0 ⫹V,
This shows the quantum interference in the time domain.
The above analysis is valid only for the case where the
considered system is isolated from an environment and not
measured by a detecting apparatus—a detector. For our purpose, we need to consider an open system S interacting with
an environment 共reservoir兲 or a detector E, and we must
extend the concepts of multiparticle 共time兲 wave functions
and the corresponding many-particle paths defined above. To
do the generalization, we first invoke the effective field operator
taking into account the role of the interaction between E and
S. Here, H E is the free Hamiltonian for E. If we only consider an ideal quantum decoherence process without dissipation, V should possess the nature of quantum nondemolition:
关 H 0 ,W 兴 ⫽0 关7,12兴.
Let the states 兩 n 典 ⬅ 兩 n V ,n H 典 be the common eigenstates of
H 0 and W corresponding to the eigenvalues E n and V(n) 关 n
⫽(n V ,n H ) 兴 . If the initial state of the total system is
012112-4
兩 ␺ 共 0 兲典 ⫽ 兩 ␾ s典 丢 兩 ␾ E典 ,
共16兲
UNDERSTANDING THE DESTRUCTION OF nTH-ORDER . . .
PHYSICAL REVIEW A 66, 012112 共2002兲
where 兩 ␾ s 典 and 兩 ␾ E 典 are some specially given initial states
of S and E, respectively, we can define the effective two-time
state vector
for a cavity QED system. The concrete calculation in Ref.
关13兴 shows that the 2-QDC effects can indeed be observed in
the proposed experiment. But it involves a dissipation effect,
losing energy. However, it is well known that quantum decoherence can still occur for an energy conserving system.
So in principle dissipation is not indispensable for a discussion about the decoherence effect. For this reason it is natural
and interesting to consider a pure decoherence process without dissipation. The pure decoherence can be well understood through the quantum entanglement of the considered
system with the environment or the measuring apparatus. For
a model with a pure decoherence process, many concepts
共such as the multiparticle path and the corresponding whichpath detection兲 can be made much clearer. Unlike the approximately solvable model treated in Ref. 关13兴, which loses
its energy and coherence simultaneously, the model proposed
in this section, a bosonic system of two modes interacting
with an external system of many harmonic oscillators, does
not dissipate its energy. This property makes the model exactly solvable, and as a result the problem of higher order
quantum decoherence can be studied in a straightforward
way.
By taking ប⫽1, the model Hamiltonian Ĥ⫽Ĥ 0 ⫹V̂ is defined by
兩 ␺ B 共 t,t ⬘ 兲 典 ⫽B̂ 共 t ⬘ 兲 B̂ 共 t 兲 兩 ␺ 共 0 兲 典
共17兲
as a reasonable generalization of the effective ‘‘two-time
wave function’’ given above. Its norm is just the secondorder correlation function
具 ␺ B 共 t,t ⬘ 兲 兩 ␺ B 共 t,t ⬘ 兲 典 ⫽Tr 关 ␳ˆ 共 0 兲 B̂ † 共 t 兲 B̂ † 共 t ⬘ 兲 B̂ 共 t ⬘ 兲 B̂ 共 t 兲兴
⫽G (2) „t,t ⬘ , ␳ˆ 共 0 兲 …
共18兲
for the density matrix ␳ˆ (0)⫽ 兩 ␺ (0) 典具 ␺ (0) 兩 .
In fact, because the nondemolition interaction does not
result in dissipation, the basic dynamic properties of the open
system do not change even in the presence of E. If we choose
兩 ␾ s 典 ⫽ 兩 1 H ,1V 典 , there are only two paths from the initial state
兩 1 V ,1H 典 to the final state 兩 0,0典 for S, and 兩 0,0典 is the unique
state which can be reached by the action of B̂(t ⬘ )B̂(t). Then,
具 ␺ B 共 t,t ⬘ 兲 兩 ␺ B 共 t,t ⬘ 兲 典 ⫽ 兺 具 ␺ B 共 t,t ⬘ 兲 兩 n, ␤ 典具 n, ␤ 兩 ␺ B 共 t,t ⬘ 兲 典
n, ␤
Ĥ 0 ⫽ ␻ V b̂ V† b̂ V ,
⫽
兺␤
⫽
兺␤ 円具 0,␤ 兩 B̂ 共 t ⬘ 兲 B̂ 共 t 兲 兩 1 H ,1V , ␾ E 典 円
⫽
円具 0,␤ 兩 ␺ B 共 t,t ⬘ 兲 典 円2
V̂⫽
2
兺␤ 兩 ⌿ ␤共 t 1 ,t 2 兲 兩 2 .
Here, the summation ranges over the complete set of states
兩 ␤ 典 of E, and each term in the sum is a norm square of the
effective two-particle wave function
⌿ ␤ 共 t 1 ,t 2 兲 ⫽ 具 0,␤ 兩 B̂ 共 t ⬘ 兲 B̂ 共 t 兲 兩 1 H ,1V , ␾ E 典
兺j ␻ j â †j â j ⫹ 兺j 关 d V共 ␻ j 兲 b̂ V† b̂ V ⫹d H共 ␻ j 兲 b̂ H† b̂ H 兴
⫻ 共 â †j ⫹â j 兲 ,
共19兲
共20兲
for the open system.
From the above calculations for the second- and thirdorder quantum decoherence, we observe that for a specially
given initial state a higher order correlation function may be
explicitly written down as the norm square 共or its sum兲 of the
multitime wave function, which is a coherent superposition
of several complex components associated with the generalized many-particle paths. It is pointed out that this kind of
many-particle path is not a simple product of single-particle
paths, but can be determined by the specially designed measurement.
IV. GENERALIZED WHICH-PATH DETECTION
IN AN INTRACAVITY MODEL
In this section, an intracavity model is presented to demonstrate in the multiparticle picture the ‘‘which-path’’ detection associated with higher order quantum decoherence.
In a recent paper 关13兴, we studied the problem of 2-QDC
共21兲
共22兲
where Ĥ 0 is the free Hamiltonian of the system, V̂ the free
Hamiltonian 兺 j ␻ j â †j â j of the reservoir 共or a detector兲 plus a
nondemolition interaction between the system and the reser†
(b̂ H ) the creation 共annihilation兲 opvoir, and b̂ V† (b̂ V ), b̂ H
erators for the two modes with frequencies ␻ V (⫽0) and
␻ H ⫽0. The operators â †j (â j ) are creation 共annihilation兲 operators of the reservoir modes of frequencies ␻ j . The
frequency-dependent constant d H ( ␻ j ) 关 d V ( ␻ j ) 兴 measures
the coupling constant between the H 关V兴 mode and the j
mode of the reservoir.
The most important feature of the model is the nondemolition condition 关 H 0 ,V 兴 ⫽0. It means that the system does
not dissipate energy to the reservoir. On the other hand, the
system can leave an imprint on the reservoir since, for different number states 兩 n V ,n H 典 , there are different interactions
兺j 关 n V d V共 ␻ j 兲 ⫹n H d H共 ␻ j 兲兴共 â †j ⫹â j 兲
acting on the oscillator reservoir with different driving forces
⬃n V d V ( ␻ j )⫹n H d H ( ␻ j ). When there is only one mode in
the external system 共reservoir兲 the whole system can physically be described by an intracavity model: A two-mode cavity field interacts with a moving wall of the cavity, which is
attached to a spring and can be regarded as a harmonic oscillator with a small mass 关4,8兴. The fields are coupled to the
012112-5
PHYSICAL REVIEW A 66, 012112 共2002兲
D. L. ZHOU, P. ZHANG, AND C. P. SUN
cavity wall 共a moving mirror兲 by the radiation pressure
†
b̂ H and b̂ V† b̂ V .
forces in proportion to the photon numbers b̂ H
For the above introduced model, we can discuss the
higher order decoherence problem in the Heisenberg picture
by explicitly defining the many-particle which-path measurement. The second-order coherence is directly determined by
the second-order correlation function
G„t,t ⬘ , ␳ˆ 共 0 兲 …⫽Tr 关 ␳ˆ 共 0 兲 B̂ † 共 t 兲 B̂ † 共 t ⬘ 兲 B̂ 共 t ⬘ 兲 B̂ 共 t 兲兴 , 共23兲
1
兩 ␺ B 共 t,t ⬘ 兲 典 ⫽ e iV̂(0,0)t ⬘ 关 exp共 ⫺i ␻ V t ⬘ 兲 e ⫺iV̂(1,0)t ⬘ e iV̂(1,0)t
2
⫹exp共 ⫺i ␻ V t 兲 e iV̂(0,0)t ⬘ e ⫺iV̂(0,1)t ⬘ e iV̂(0,1)t 兴
⫻e ⫺iV̂(1,1)t 兩 兵 0 j 其 典 丢 兩 0 H ,0V 典
of two components for the two paths from the initial twoparticle state 兩 1 H ,1V 典 to the two-particle vacuum 兩 0 H ,0V 典 . It
should be noticed that the effective actions of the reservoir
which is defined as a functional of the density operator ␳ˆ (0)
of the whole system at a given time 0. Here, the bosonic field
共measuring兲 operator
V̂ 共 m,n 兲 ⬅
B̂ 共 t 兲 ⫽exp共 iV̂t 兲关 c H b̂ H ⫹c V b̂ V exp共 ⫺i ␻ V t 兲兴 exp共 ⫺iV̂t 兲
共24兲
⫽
is defined for the interacting system. Like the operator defined for the noninteracting system, it also describes a specific destructive quantum measurement 关4兴 with respect to
the polarized states
* 兩 H 典 ⫹c V* 兩 V 典 ,
兩 ⫹ 典 ⫽c H
where c H and c V satisfy the normalization relation 兩 c H 兩 2
⫹ 兩 c V 兩 2 ⫽1. Without loss of generality, we take c H ⫽c V
⫽1/冑2, considering a specific measuremeant.
To examine whether the macroscopic feature of the reservoir causes the second-order decoherence or not, we consider
the whole system in an initial state
兩 ␺ 共 0 兲 典 ⫽ 兩 1 H ,1V 典 丢 兩 兵 0 j 其 典 ,
兺j V̂ j 共 m,n 兲
兺j ␻ j â †j â j ⫹ 兺j 关 d V共 ␻ j 兲 m⫹d H共 ␻ j 兲 n 兴共 â †j ⫹â j 兲
共29兲
can label the different paths and record the path information
in the reservior. Thus, this generalized which-path measurement leads to second-order quantum decoherence.
The above result clearly demonstrates that, with the presence of the reservoir, the different probability amplitudes
关 ⬃exp(⫺i␻V t⬘) and exp(⫺i␻V t)兴 from 兩 1 H ,1V 典 to 兩 0 H ,0V 典
entangle with the different states
1 iV̂(0,0)t ⫺iV̂(1,0)t iV̂(1,0)t ⫺iV̂(1,1)t
⬘e
⬘e
e
e
兩兵0 j其典
2
and
共25兲
where 兩 兵 0 j 其 典 is the vacuum state of the reservoir. Here, we
have denoted the general Fock states of the many-mode field
by 兩 兵 n j 其 典 ⬅ 兩 n 1 ,n 2 , . . . 典 . Because the present discussion
concerns an external system interacting with the considered
system, the concepts presented in the last section must be
alternated. Actually, instead of the effective ‘‘two-time wave
function,’’ we use the effective two-time state vector
共28兲
1 iV̂(0,0)t ⫺iV̂(0,1)t iV̂(0,1)t ⫺iV̂(1,1)t
⬘e
⬘e
e
e
兩兵0 j其典
2
of the reservoir. This is just the physical cause of secondorder quantum decoherence. In the following section an explicit calculation of the second-order correlation function
will be given to illustrate this crucial observation.
V. DYNAMIC DECOHERENCE IN HIGHER ORDER CASE
兩 ␺ B 共 t,t ⬘ 兲 典 ⫽B̂ 共 t ⬘ 兲 B̂ 共 t 兲 兩 ␺ 共 0 兲 典 .
共26兲
Then we can rewrite the second-order correlation function as
G„t,t ⬘ , ␳ˆ 共 0 兲 …⫽ 具 ␺ B 共 t,t ⬘ 兲 兩 ␺ B 共 t,t ⬘ 兲 典 .
After a straightforward calculation the second-order correlation function can be expressed in a factorization form 关9兴
共27兲
It is interesting that the effective state vector can be evaluated as the superposition
G„t,t ⬘ , ␳ˆ 共 0 兲 …⫽
冋 冉
1
1⫹Im e i ␻ V (t⫺t ⬘ )
2
冊册
,
共30兲
where each factor
F j ⫽ 具 0 j 兩 e iV̂ j (1,1)t e ⫺iV̂ j (0,1)t e iV̂ j (0,1)t ⬘ e ⫺iV̂ j (1,0)t ⬘ e iV̂ j (1,0)t e ⫺iV̂ j (1,1)t 兩 0 j 典 ⬅ 具 0 j 兩 û 6j 共 t 6 兲 兩 0 j 典
is a two-time transition amplitude of the jth mode of the
reservoir. Obviously, the term 兿 j F j measures the extent of
coherence and decoherence in the second-order case. It plays
兿j F j
共31兲
the same role as the decoherence factor of first-order decoherence 关7兴, so it is also called the decoherence factor.
In the following, to give the factor F j explicitly. We adopt
012112-6
UNDERSTANDING THE DESTRUCTION OF nTH-ORDER . . .
PHYSICAL REVIEW A 66, 012112 共2002兲
the Wei-Norman method 关17,18兴 to calculate the effective
time evolution defined by û 6j (t 6 ). It can be imagined as an
evolution governed by a discrete time-dependent Hamiltonian H(t) dominated by V̂ j (1,1), ⫺V̂ j (1,0), V̂ j (1,0),
⫺V̂ j (0,1), V̂ j (0,1), and ⫺V̂ j (1,1) in six time intervals 关 t 0
⫽0,t 1 ⫽t 兴 , 关 t 1 ,t 2 ⫽2t 兴 , 关 t 2 ,t 3 ⫽2t⫹t ⬘ 兴 , 关 t 3 ,t 4 ⫽2t⫹2t ⬘ 兴 ,
关 t 4 ,t 5 ⫽3t⫹2t ⬘ 兴 , 关 t 5 ,t 6 ⫽4t⫹2t ⬘ 兴 , respectively. In the kth
step of calculation, we take the final state of the (k⫺1)th
step as its initial state. Therefore, we obtain û 6j (t 6 ) as the
sixth-step evolution
as N→⬁ since 兺 Nj⫽1 R j (t,t ⬘ ) is a diverging series or a monotonically increasing function of t⫺t ⬘ under some reasonable
conditions.
In order to demonstrate the above conclusion quantitatively, we give the numerical results for the second-order
decoherence for different numbers N of the quantum oscillators. As N increases, these results are illustrated in Fig. 1. In
the numerical calculation, the coupling constants 兵 d V ( j) 其
take random values in the domain 关 0.8,1.0兴 , the coupling
constants 兵 d H ( j) 其 in 关 0.2,0.4兴 , and the frequencies 兵 ␻ j 其 in
关 0.5,1.5兴 . The other parameters are given in the caption of
the figure.
From both the graphic illustrations given by the numerical
calculation and the analytic result given by Eqs.
共30兲,共33兲,共34兲 , we see clearly that the second-order correlation function depends not only on the time interval t ⬘ ⫺t, but
also on t or t ⬘ . In fact it follows from the analytic result
6
†
6
û 6j 共 t 6 兲 ⫽e g 1 j (t 6 )â j e g 2 j (t 6 )â j
† â
6
6
j g 3 j (t 6 )â j g 4 j (t 6 )
e
e
共32兲
.
Here, g 6k j (t 6 ) (k⫽1,2,3,4) are the coefficients that can be
explicitly obtained. But for the calculation of the jth component
F j ⫽exp关 g 64 j 共 t 6 兲兴
冉
共33兲
Im e i ␻ V (t⫺t ⬘ )
of the decoherence factor, we only need to know g 64 j . The
detailed discussion in the Appendix gives
g 64 j 共 t 6 兲 ⫽⫺
⫹
2
␻ 2j
i
␻ 2j
关 d H 共 j 兲 ⫺d V 共 j 兲兴 2 sin2
冋
1
␻ 共 t ⬘ ⫺t 兲
2 j
册
2
关 d V2 共 j 兲 ⫺d H
共 j 兲兴 „␻ j 共 t ⬘ ⫺t 兲
⫹2 兵 1⫺cos共 ␻ j 关 t ⬘ ⫺t 兴 兲 其 sin ␻ j t
⫹ 共 1⫺2 cos ␻ j t 兲 sin共 ␻ j 关 t ⬘ ⫺t 兴 兲 …
⫽⫺R j 共 t⫺t ⬘ 兲 ⫹i⍀ j 共 t,t ⬘ 兲 .
共34兲
It is noticed that the real part
冋
1
␻ 共 t ⬘ ⫺t 兲
⫺R j 共 t⫺t ⬘ 兲 ⫽⫺ 2 关 d H 共 j 兲 ⫺d V 共 j 兲兴 sin
2 j
␻j
2
2
2
册
N
兿
j⫽1
N
F j⫽
兿
N
e i⍀ j (t,t ⬘ )
j⫽1
兿
e ⫺R j (t⫺t ⬘ )
j⫽1
⫽ 兩 F 兩 exp关 i⍀ 共 t,t ⬘ 兲兴
implies the vanishing of the second-order correlation in the
macroscopic limit that the number N of particles making up
the reservoir approaches infinity. This is because
冋
兩 F 兩 ⫽exp ⫺
N
兺
j⫽1
册
R j 共 t,t ⬘ 兲 →0
冊
1
⫽ 兩 F 兩 cos关 ␻ V 共 t⫺t ⬘ 兲 ⫹⍀ 共 t,t ⬘ 兲兴
2
共35兲
that the amplitude of the second-order correlation function is
mainly determined by the time interval t ⬘ ⫺t, but the phase is
determined by the two-time parameters. What is more important is that, as the number of quantum oscillators increases,
the second-order coherence vanishes faster and faster, and
the amplitude for quantum revival becomes smaller and
smaller. With a reasonable extrapolation, it can be predicted
that, when the number of quantum oscillators approaches
infinity in the macroscopic limit, the second-order coherence
will vanish in a very short time and thus no quantum revival
phenomenon can be observed.
VI. CONCLUDING REMARKS
only depends on the time interval t ⬘ ⫺t, but the imaginary
part ⍀ j (t,t ⬘ ) depends on both t ⬘ and t ⬘ as a two-time function.
Because ⫺R j cannot exceed zero, the norm 兩 F j 兩
⫽e ⫺R j (t) of the factor F j cannot exceed 1. Then from the
arguments about the first-order decoherence in our previous
works on quantum measurement theory 关7兴, it is concluded
qualitatively that the factorization structure of the decoherence factor
F⫽
兿j F j
In this paper we first depict the high order quantum coherence of a boson system by introducing the concept of the
multiparticle wave amplitude. For some cases with a specifically given initial state, we show that the norm square of the
multiparticle wave amplitude 共or a sum of the norm squares
for an open system兲 gives a high order correlation function.
As an effective multitime wave function, this amplitude can
be shown to be a superposition of several multiparticle paths.
When the environment or an apparatus entangles with them
to form a generalized which-path共way兲 measurement, high
order quantum decoherence happens dynamically. Some explicit and general illustrations are presented in this paper to
illustrate our observation. But to prove our conjecture that
any high order correlation function indicating the existence
of high order quantum coherence can be expressed as the
norm square of a properly defined effective wave amplitude
for a many-particle system, there is still a long way to go. If
this conjecture is true under certain general conditions, then
there still exists the problem of clarifying these conditions.
Moreover, experimental proposals that can be implemented
at least in principle are still unavailable.
Our present investigations shed light on the understanding
of quantum coherence. According to arguments in this paper,
012112-7
PHYSICAL REVIEW A 66, 012112 共2002兲
D. L. ZHOU, P. ZHANG, AND C. P. SUN
with certain initial states, the high order quantum coherence
of systems can be described as a generalized interference
phenomenon of two multiparticle paths. For these specifically prepared systems, beyond the classical analog reflected
by the spatial interference of two paths in a classical electromagnetic field, the intrinsically quantum features 共higher order ones兲 of coherence may be theoretically understood in a
unified framework. In this sense, as an essential element, the
which-path共way兲 detection in both the original and the extended versions naturally provides a more complete description for the decoherence mechanism in quantum measurement and the transition from quantum to classical mechanics.
ACKNOWLEDGMENTS
This work is supported by the NSF of China and the
Knowledge Innovation Program 共KIP兲 of the Chinese Academy of Science. X. F. Liu is acknowledged for his kind patience in reading this manuscript.
APPENDIX
In this appendix, the Wei-Norman method 关17,18兴 is
adopted to calculate the second-order decoherence factor F j .
The calculation is completed in six steps.
During the time period 关 t k⫺1 ,t k 兴 (k⫽1,2, . . . ,6), let
W kj (t,t ⬘ ) be the time evolution dominated by the singleparticle Hamiltonian
ĥ kj ⫽ ␣ kj â †j â j ⫹ ␤ kj â †j ⫹ ␥ kj â j
兵 k⫽1,2, . . . ,6其 .
共A1兲
The coefficients ␣ kj , ␤ kj , ␥ kj and the time intervals T k ⫽t k
⫺t k⫺1 take different values in the six different steps:
␣ 1j ⫽ ␻ j ,
␤ 1j ⫽ ␥ 1j ⫽d V 共 ␻ j 兲 ⫹d H 共 ␻ j 兲 ,
␣ 2j ⫽⫺ ␻ j ,
␣ 3j ⫽ ␻ j ,
␤ 3j ⫽ ␥ 3j ⫽d V 共 ␻ j 兲 ,
␣ 4j ⫽⫺ ␻ j ,
␤ 4j ⫽ ␥ 4j ⫽⫺d H 共 ␻ j 兲 ,
␣ 5j ⫽ ␻ j ,
␣ 6j ⫽ ␻ j ,
␤ 2j ⫽ ␥ 2j ⫽d V 共 ␻ j 兲 ,
␤ 5j ⫽ ␥ 5j ⫽d H 共 ␻ j 兲 ,
T 1 ⫽t,
T 2 ⫽t,
T 3 ⫽t ⬘ ,
T 4 ⫽t ⬘ ,
T 5 ⫽t,
␤ 6j ⫽ ␥ 6j ⫽⫺d V 共 ␻ j 兲 ⫺d H 共 ␻ j 兲 ,
T 6 ⫽t.
共A2兲
Because of the fact that the four operators n j ⫽â †j â j , â †j , â j ,
and 1 form a closed algebra—the Heisenberg-Wely—
algebra, the unitary time evolution operator at each step
takes the following form 共Wei-Norman theorem兲:
k
†
k
û kj 共 T 兲 ⫽e g 1 j (T)â j e g 2 j (T)â j
FIG. 1. The horizontal axis denotes the time period t ⬘ ⫺t, in
units of 1/␻ V . The vertical axis denotes the second-order correlation function G⬅G„t,t ⬘ , ␳ˆ (0)…. Parameters ␻ V ⫽1.0, 共a兲 N⫽5, t
⫽0, 共b兲 N⫽5,t⫽5, 共c兲 N⫽10,t⫽0, 共d兲 N⫽10,t⫽5.
† â
k
k
j g 3 j (T)â j g 4 j (T)
e
e
共A3兲
for T苸 关 t k⫺1 ,t k 兴 in a special sequence. Here the coefficients
g ks j (T) (s⫽1,2,3,4) are functions of T to be determined. The
benefit of the above form is that only the coefficient g k4 j (T)
is needed in the calculation of the average value at the
vacuum state. So we can greatly reduce the complexity of
our calculation as we need to pay attention only to things
concerning g k4 j (T).
Substituting û kj (T) into the Schrödinger equation
012112-8
PHYSICAL REVIEW A 66, 012112 共2002兲
UNDERSTANDING THE DESTRUCTION OF nTH-ORDER . . .
i
冉
d k
û ⫽ĥ kj û kj ,
dT j
g k1 j 共 T 兲 ⫽ g k1 j 共 t k⫺1 兲 ⫹
we find the coefficients g ks j (T) (s⫽1,2,3,4) satisfy the following system of equations:
g k4 j 共 T 兲 ⫽g k4 j 共 t k⫺1 兲 ⫹
d k
g ⫽⫺i ␣ kj ,
dT 2 j
␥ kj
␣ kj
␤ kj
␣k
冉
冊
k
e ⫺i ␣ j (T⫺t k⫺1 ) ⫺
g k1 j 共 t k⫺1 兲 ⫹
k
⫻ 共 e ⫺i ␣ j (T⫺t k⫺1 ) ⫺1 兲 ⫹i
␤ kj
␣ kj
冊
␤ kj
␣ kj
,
␤ kj ␥ kj 共 T⫺t k⫺1 兲
␣ kj
共A6兲
Notice that, to obtain the above result, we have used the
initial conditions
d k
d k
g 1 j ⫺g k1 j
g ⫽⫺i ␤ kj ,
dT
dT 2 j
g k1 j 共 t k⫺1 兲 ⫽g k⫺1
1 j 共 t k⫺1 兲 ,
e
k
⫺g 2 j
d k
g ⫽⫺i ␥ kj ,
dT 3 j
d k
k d
g 4 j ⫺g k1 j e ⫺g 2 j
g k ⫽0.
dT
dT 3 j
共A4兲
g k1 j 共 t k 兲 ⫽
冉
g k⫺1
1 j 共 t k⫺1 兲 ⫹
g k4 j 共 t k 兲 ⫽g k⫺1
4 j 共 t k ⫺1 兲 ⫹
d k
g ⫽⫺i ␥ kj g k1 j
dT 4 j
共A7兲
共A8兲
g k4 j 共 t k⫺1 兲 ⫽g k⫺1
4 j 共 t k⫺1 兲
for each step and the initial conditions g 01 j (t 0 )⫽g 04 j (t 0 )⫽0
for the first step. Then, we obtain a set of iteration equations
Using the results
d k
g ⫽⫺i ␣ kj g k1 j ⫺i ␤ kj ,
dT 1 j
.
共A5兲
⫹i
obtained by simplifying the above system of equations, we
get the solution
关1兴 R.J. Glauber, Phys. Rev. 130, 2529 共1963兲; 131, 2766 共1963兲.
关2兴 H. Hanburg-Brow and R.Q. Twiss, Philos. Mag. 45, 663
共1954兲; Nature 共London兲 178, 1046 共1956兲; Proc. R. Soc. London, Ser. A 242, 300 共1957兲.
关3兴 S. Durt, T. Nonn, and G. Rampe, Nature 共London兲 395, 33
共1998兲.
关4兴 E. Buks, R. Schuster, M. Heiblum, D. Mahalu, and V. Umansky, Nature 共London兲 391, 871 共1998兲.
关5兴 W.H. Zurek, Phys. Today, 44 共10兲, 36 共1991兲.
关6兴 M. Brune, E. Hagley, J. Dreyer, X. Maitre, A. Maali, C.
Wunderlich, J.M. Raimond, and S. Haroche, Phys. Rev. Lett.
77, 4887 共1996兲.
关7兴 C.P. Sun, Phys. Rev. A 48, 898 共1993兲; C.P. Sun, Chin. J. Phys.
共Taipei兲 32, 7 共1994兲; C.P. Sun, X.X. Yi, and X.J. Liu, Fortschr.
Phys. 43, 585 共1995兲.
关8兴 S. Bose, K. Jacobs, P. Knight, Phys. Rev. A 82, 3204 共1999兲.
关9兴 W. Unruh, Phys. Rev. A 51, 992 共1995兲.
关10兴 G. Palma, K. Suominen, and A. Ekert, Proc. R. Soc. London,
Ser. A 452, 567 共1996兲.
关11兴 C.P. Sun, H. Zhan, and X.F. Liu, Phys. Rev. A 58, 1810 共1998兲.
关12兴 C.P. Sun, X.F. Liu, D.L. Zhou, and S.X. Yu, Phys. Rev. A 63,
␥ kj
␣ kj
冉
␤ kj
␣ kj
冊
e
⫺i ␣ k T k
g k⫺1
1 j 共 t k⫺1 兲 ⫹
⫺
␤ kj
␣ kj
冊
␤ kj
␣ kj
,
k
共 e ⫺i ␣ j T k ⫺1 兲
␤ kj ␥ kj T k
.
共A9兲
␣k
Iterating six times with different initial conditions and coefficients, the final result of g 64 (t 6 ) is obtained as Eq. 共A9兲.
关13兴
关14兴
关15兴
关16兴
012111 共2001兲; C.P. Sun, D.L. Zhou, S.X. Yu, and X.F. Liu,
Eur. Phys. J. D 13, 145 共2001兲; C.P. Sun, X.F. Liu, D.L. Zhou,
and S.X. Yu, ibid. 17, 89 共2001兲.
D.L. Zhou and C.P. Sun, LNAL report, 2001, e-print
quant-ph/0104038.
M.O. Scully and M.S. Zubairy, Quantum Optics 共Cambridge
University Press, Cambridge, England, 1997兲, pp. 97–129.
Y. Shih, Adv. At., Mol., Opt. Phys. 41, 1 共1999兲.
This definition, which is given by J.R. Klauder and E.C.G.
Sudarshan, Fundamentals of Quantum Optics 共W.A. Benjamin,
New York, 1968兲, more convenient to describe coherence as
interference, is a little different in the denominator from
Glauber’s. Glauber’s original definition is
g共␣1 ,␣2 , . . . , ␣ n ; ␤ 1 , ␤ 2 , . . . , ␤ n 兲
⫽ Tr关 ␳ˆ B ␤† 1 共 t 1 兲 B †␤ 2 共 t 2 兲 •••B ␤† n 共 t n 兲 B ␣ n 共 t n 兲 •••
B ␣ 2 共 t 2 兲 B ␣ 1 共 t 1 兲兴 / 冑G 共 ␣ 1 ,t 1 兲 G 共 ␣ 2 ,t 2 兲 •••G 共 ␣ n ,t n 兲
冑G 共 ␤ 1 ,t 1 兲 G 共 ␤ 2 ,t 2 兲 •••G 共 ␤ n ,t n 兲 .
关17兴 J. Wei and E. Norman, J. Math. Phys. 4A, 575 共1963兲.
关18兴 C.P. Sun and Q. Xiao, Commun. Theor. Phys. 16, 359 共1990兲.
012112-9