* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Divergence Theorem §17.3 - Math
Survey
Document related concepts
Time in physics wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Circular dichroism wikipedia , lookup
Electromagnetism wikipedia , lookup
Magnetic monopole wikipedia , lookup
Four-vector wikipedia , lookup
Vector space wikipedia , lookup
Electromagnet wikipedia , lookup
Superconductivity wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Noether's theorem wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electrostatics wikipedia , lookup
Lorentz force wikipedia , lookup
Transcript
Divergence Theorem
§17.3
11 December 2013
Fundamental Theorem, Four Ways.
Rb
I
F 0 (x) dx = F (b) − F (a)
[a, b]
I
If C path from P to Q,
φ on boundary of C
I
Green’s Theorem:
RR
I
Stokes’s Theorem:
RR
a
R
C
F (x) on boundary of
(∇φ) · ds = φ(Q) − φ(P)
curlz (F) dA =
R
S
R
curl(F) · dS =
∂R
F · ds
R
∂S
F · ds
Every time:
Integral of a derivative of something over some domain equals
the integral of the original over the boundary of the domain.
3D Fundamental Theorem.
Say R is a 3D region, with boundary surface ∂R, oriented with
outward pointing normal.
ZZZ
ZZ
(???) dV =
F · dS
R
∂R
The derivative to use is the divergence:
Definition
Given a vector field F = hF1 , F2 , F3 i, the divergence is
div F = ∇ · F = h∂x , ∂y , ∂z i · hF1 , F2 , F3 i = F1x + F2y + F3z .
Divergence Theorem
ZZZ
ZZ
F · dS.
div F dV =
R
∂R
Example.
Example: Calculate the flux of F(x, y , z) = hx + y , x − z, z 2 i
through the boundary of the cube −1 ≤ x, y , z ≤ 1, oriented
positively (with outward pointing normals).
Example.
Example: Calculate the flux of F(x, y , z) = hx + y , x − z, z 2 i
through the boundary of the cube −1 ≤ x, y , z ≤ 1, oriented
positively (with outward pointing normals).
Remark: The surface integral is not difficult, but requires
taking care of the cube’s 6 separate faces.
If F would happen to be a curl vector field, then we would
know the flux is zero; however F is NOT a curl vector field
(can you figure out why not?). So, that shortcut is not
available for this example.
Example.
Example: Calculate the flux of F(x, y , z) = hx + y , x − z, z 2 i
through the boundary of the cube −1 ≤ x, y , z ≤ 1, oriented
positively (with outward pointing normals).
Remark: The surface integral is not difficult, but requires
taking care of the cube’s 6 separate faces.
If F would happen to be a curl vector field, then we would
know the flux is zero; however F is NOT a curl vector field
(can you figure out why not?). So, that shortcut is not
available for this example.
Answer:
ZZ
ZZZ
F · dS =
div F dV
∂C
C
Z 1Z 1Z 1
1
2 =
(1 + 0 + 2z) dx dy dz = 4(z + z ) = 8.
−1
−1
−1
−1
Why Divergence Theorem Is True.
Let’s see why the Divergence Theorem works in the 2D case.
I C : simple closed curve in R2
I enclosing region R with positive orientation
(counterclockwise)
I parametrized by c(t) = (x(t), y (t)).
I
I
Then c0 (t) = hx 0 (t), y 0 (t)i
outward-pointing normal: n(t) = hy 0 (t), −x 0 (t)i
n
n
c0
c0
n
c0
Explanation, continued.
The flux of F across C is
Z
Z
F · n ds = hF1 , F2 i · hy 0 (t), −x 0 (t)i dt
C
ZC
=
F1 dy − F2 dx
C
Z
= h−F2 , F1 i · ds
ZCZ
=
curlz (h−F2 , F1 i) dA
(Green’s Theorem)
R
ZZ
=
(F1x + F2y ) dA.
{z }
R|
div(F)
Example.
Example: Verify the Divergence Theorem for
F(x, y , z) = hxz, x, z 2 i and the cylinder W given by
0 ≤ x 2 + y 2 ≤ 9, 0 ≤ z ≤ 6.
Answer: First, compute the flux of F across ∂W (with
outward pointing normals):
I Top surface W1 : 0 ≤ x 2 + y 2 ≤ 9, z = 6, n = h0, 0, 1i.
So F · n = z 2 = 36.
ZZ
ZZ
Flux =
F · dS =
36 dA = 36 Area(W1 )
W1
W1
= 36 · 9π = 324π
I
Bottom surface W3 : 0 ≤ x 2 + y 2 ≤ 9, z = 0,
n = h0,RR
0, −1i. So F ·RR
n = −z 2 = 0,
flux = W3 F · dS = W3 0 dA = 0.
Example, continued.
Side surface W2 , parametrized by
(x, y , z) = (3 cos θ, 3 sin θ, z), 0 ≤ θ ≤ 2π, 0 ≤ z ≤ 6:
Tθ = h−3 sin θ, 3 cos θ, 0i,
Tz = h0, 0, 1i,
n = h3 cos θ, 3 sin θ, 0i
So,
Z
2π
Z
6
h3z cos θ, 3 cos θ, z 2 i · h3 cos θ, 3 sin θ, 0i dθ
flux =
0
Z
0
2π
Z
=
0
6
9z cos2 θ + 9 cos θ sin θ dz dθ
0
= · · · = 162π.
Therefore the total flux is 324π + 0 + 162π = 486π.
Example, concluded.
Alternatively, find the divergence:
∇ · F = z + 0 + 2z = 3z,
so
ZZ
ZZZ
F · dS =
flux =
∇ · F dV
∂W
(Divergence Theorem)
W
Z
6
ZZ
=
3z dx dy dz
0≤x 2 +y 2 ≤9
0
Z
6
3z · Area(0 ≤ x 2 + y 2 ≤ 9) dz
0
1 2 6
= 27π · z 2 0
= 27π · 18
= 486π.
=
Physical Interpretation.
If F represents the velocity of a fluid flow and S is a closed
surface, then the flux of F across S represents the amount of
fluid leaving or entering S.
The divergence of F represents the flow rate (or flux) per unit
volume.
I
If div(F)P > 0 it means there is net “creation” of the
fluid near P.
I
If div(F)P < 0 it means there is net “destruction” of the
fluid near P.
Clicker Question:
Moving from the picture on the left to the picture on the
right, what are the signs of ∇ · F?
A.
B.
C.
D.
positive, positive, negative
zero, positive, negative
positive, negative, zero
zero, negative, positive
receiver channel: 41
session ID: bsumath275
Clicker Question:
True or False? The vector field F is defined everywhere in a
region W bounded by a surface S. If ∇ · F > 0 at all points of
W , then the vector field F points outward at all points of S.
A. True, and I am very confident.
B. True, but I am not very confident.
C. False, but I am not very confident.
D. False, and I am very confident.
receiver channel: 41
session ID: bsumath275
Div, Grad, Curl.
I
If φ is a scalar-valued function,
grad φ = ∇φ = h∂x , ∂y , ∂z iφ =
∂φ ∂φ ∂φ
,
,
∂x ∂y ∂z
The result is a vector field.
I
If F is a vector field,
curl F = ∇×F = h∂x , ∂y , ∂z i×hF1 , F2 , F3 i = hF3y −F2z , . . .i
The result is a vector field.
I
If F is a vector field,
div F = ∇ · F = h∂x , ∂y , ∂z i · hF1 , F2 , F3 i = F1x + F2y + F3z
The result is a scalar-valued function.
Clicker Question:
If F(x, y , z) is a vector field and f (x, y , z) is a scalar function,
which of the following is not defined?
A. ∇f
B. ∇ · F + f
C. F + ∇f
D. ∇ · F + ∇f
E. More than one of the above
F. None of the above
receiver channel: 41
session ID: bsumath275
Clicker Question:
If F(x, y , z) is a vector field and f (x, y , z) is a scalar function,
which of the following quantities is a vector?
A. ∇ · F
B. ∇f · u~
C. ∇ · ∇f
D. (∇ · F)F
receiver channel: 41
session ID: bsumath275
Notice: If F is a curl vector field, F = ∇ × A, then its
divergence is zero:
∇ · (∇ × A) = 0
div(curl A) = 0
This is like ∇ × (∇φ) = 0.
I
Just like checking cross-partials is a test for exactness, we
can use divergence to test whether F is a curl vector field.
I
Interesting connections to further topics in math:
geometry, topology
Worksheet.
Worksheet #1–3
Clicker Question:
What is the divergence of the vector field hx 2 , y − e z , y − 2zxi?
A. 0
B. 1
C. −1
D. h2x, 1, −2xi
E. h1 + e z , 2z, 0i
receiver channel: 41
session ID: bsumath275
Maxwell’s Equations, First Two.
Maxwell’s equations describe electricity and magnetism.
They revolutionized science and mathematics.
I
The divergence of the electric field is the charge density:
∇ · E = q.
(Sources and sinks of the electric field are given by
charged particles.)
In other words, the flux of the electric field through any
closed surfaceRR
is equal to the total charge enclosed inside
that surface: ∂W E · dS = charge inside W .
I
The divergence of the magnetic field is zero: ∇ · B = 0.
There are no magnetic monopoles. The flux of the
magnetic
field through any closed surface is zero:
RR
B
·
dS
= 0.
∂W
(For simplicity, leaving out some constant factors.)
Maxwell’s Equations, Last Two.
I
The time derivative of the magnetic field is the current
plus the curl of the electric field: ∂B
= J + ∇ × E.
∂t
A changing magnetic field induces both current and
electric field.
I
The time derivative of the electric field is the opposite of
= −∇ × B.
the curl of the magnetic field: ∂E
∂t
A changing electric field induces a magnetic field.
∇·E=q
∇·B=0
∂B
=J +∇×E
∂t
∂E
= −∇ × B
∂t
RR
∂W
E · dS = charge inside W
RR
B · dS = 0
∂W








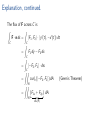


















![Homework on FTC [pdf]](http://s1.studyres.com/store/data/008882242_1-853c705082430dffcc7cf83bfec09e1a-150x150.png)





