Download RL-series circuits solutions

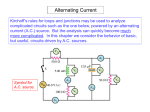
RL-series circuits
Math 2410
Spring 2011
Consider the RL-series circuit shown in the figure below, which contains a counterclockwise
current I = I(t), a resistance R, and inductance L, and a generator that supplies a voltage V (t)
when the switch is closed. Kirchhoff’s voltage law satates that, “the algebraic sum of all voltage
R
V (t)
I = I(t)
L
drops around an electric circuit is zero.” Applied to this RL-series circuit, the statement translates
to the fact that the current I = I(t) in the circuit satisfies the first-order linear differential equation
LI˙ + RI = V (t),
where I˙ denotes the derivative of I with respect to t. Substituting
obtain our usual form of a first-order nonhomogeneous equation:
dI
dt
for I˙ and dividing by L, we
R
1
dI
+ I = V (t).
dt
L
L
For convenience, we present an index of units and symbols commonly used in this theory.
Quantity
Unit
Symbol
Resistance
ohm
R
Inductance
Capacitance
henry
farad
L
C
Voltage
volt
V
Current
ampere
I
Charge
coulomb
Q
Time
seconds
sec
Table 1: Table of Units
Battery
Resistor
Inductor
Capacitor
Switch
Table 2: Symbols of Circuit Elements
Exercises
1. Use the method of integration factors to calculate what the general solution is for this
differential equation.
Solution. The integrating factor is µ(t) = e
I(t) =
R
R
L
1 −Rt
e L
L
dt
Z
R
= e L t , so we have
R
V (t)e L t dt.
In particular, if V (t) = V0 is some constant voltage, then we may evaluate the integral on
the right directly to get
Z
R
R
R
1 −Rt
1 −Rt L
V0
t
t
L
L
L
L
I(t) = e
V0 e dt = e
V0 e + c =
+ ce− L t .
L
L
R
R
2. In an RL-series circuit, L = 4 henries, R = 5 ohms, V = 8 volts, and I(0) = 0 amperes.
Find the current at the end of 0.1 seconds. What will the current be after a very long time?
Solution. Using the formula from the last solution,
Z
5
5
1 5
1 5 32 5 t
8
I(t) = e− 4 t 8e 4 t dt = e− 4 t
e 4 + c = + ce− 4 t .
4
4
5
5
Using the initial condition I(0) = 0, we get c = − 85 , so
I(t) =
Then I(0.1) ≈ 0.188 and I(t) →
8
5
5
8
(1 − e− 4 t ).
5
as t → ∞.
3. Assume that the voltage V (t) is given by V0 sin(ωt), where V0 and ω are given constants.
Find the solution of the differential equation above subject to the initial condition I(0) = I0 .
Solution. I’ll give the argument using the method of undetermined coefficient here, as it is
different from the method done in class and it represents something new that you learned.
So a solution to this DE is of the form yh (t) + yp (t). First,
Ih (t) = e−
R
R
L
dt
R
= ke− L t .
Then, to find the particular solution Ip (t), we try Ip (t) = α cos(ωt) + β sin(ωt). Substituting
this into the DE, multiplying through by L to get rid of the fractions, and combining like
terms, we get
(βωL + Rα) cos(ωt) + (−αωL + Rβ) sin(ωt) = V0 sin(ωt).
Thus we have the system
Rα + βωL = 0
−αωL + Rβ = V0 .
The first equation immediately gives α = −βωLR−1 . Then, plugging this into the second
equation gives
βωL
ωL + Rβ = V0
R
2 2
ω L
+ Rβ = V0
β
R
β=
Then
α=−
V0 R
2
ω L2 +
Hence
R
I(t) = ke− L t −
V0
V0 R
= 2 2
.
ω L + R2
+R
ω 2 L2
R
R2
·
V0 ωL
2
ω L2 + R2
ωL
V0 ωL
=− 2 2
.
R
ω L + R2
cos(ωt) +
V0 R
2
ω L2 +
R2
sin(ωt).
It remains to solve for k using the initial condition I(0) = I0 . We have
I(0) = I0 = k −
V0 ωL
V0 ωL
=⇒ k = I0 + 2 2
.
ω 2 L2 + R2
ω L + R2
Thus
I(t) = Ih (t) + Ip (t) =
I0 +
V0 ωL
2
ω L2 + R2
R
e− L t −
V0 ωL
2
ω L2 + R2
cos(ωt) +
V0 R
2
ω L2 +
R2
sin(ωt).
4. Given that L = 3 henries, R = 6 ohms, V (t) = 3 sin(t), and I(0) = 10 amperes, compute
the value of the current at any time t.
Solution. Using the equation from above, we have V0 ωL = 3 · 3 = 9, V0 R = 3 · 6 = 18, and
ω 2 L2 + R2 = 12 32 + 62 = 45, so
I(t) =
459 −2t 1
2
e
− cos(t) + sin(t).
45
5
5
References
[1] N. Finizio and G. Ladas, Ordinary Differential Equations with Modern Applications, 3rd
edition, Simon & Schuster Custom Publishing, Boston, 1999.